
| A. | (-$\frac{1}{3}$,+∞) | B. | ($\frac{1}{3}$,1) | C. | (-∞,-$\frac{1}{3}$) | D. | (-1,-$\frac{1}{3}$) |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 4或-4 | C. | -2 | D. | -2或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
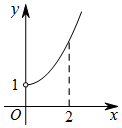 已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x),x∈R是奇函数,其部分图象如图所示,则在(-1,0)上与函数f(x)的单调性相同的是( )| A. | $y=x+\frac{1}{x}$ | B. | y=log2|x| | ||
| C. | $y=\left\{{\begin{array}{l}{e^x}&{x≥0}\\{{e^{-x}}}&{x<0}\end{array}}\right.$ | D. | y=cos(2x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )
一线性规划问题的可行域为坐标平面上的正八边形ABCDEFGH及其内部(如图),已知目标函数z=3+ax+by(a,b∈R)的最大值只在顶点B处,如果目标函数变成z=3-bx-ay时,最大值只在顶点( )| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $1+\sqrt{5}$ | B. | $2+\sqrt{5}$ | C. | $1+2\sqrt{5}$ | D. | $2+2\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com