
 (a为实常数).
(a为实常数). 上有解,求实数a的取值范围;
上有解,求实数a的取值范围; ,它的前n项和为Sn,求证:
,它的前n项和为Sn,求证: .
. ,1]上有解,可转化为方程a=x-x3在区间[
,1]上有解,可转化为方程a=x-x3在区间[ ,1]上有解,构造函数h(x)利用导数法求出函数的值域,即可得到实数a的取值范围;
,1]上有解,构造函数h(x)利用导数法求出函数的值域,即可得到实数a的取值范围; +
+ (
( ),在进行求和,从而进行证明;
),在进行求和,从而进行证明;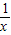 -1,(x>0),
-1,(x>0), ,
, ,
, 上求最值问题,
上求最值问题, ,
, 时,h′(x)<0,h(x)为减函数;
时,h′(x)<0,h(x)为减函数; 时,h′(x)>0,h(x)为增函数;
时,h′(x)>0,h(x)为增函数; )=
)= ,
, )=
)= ,
, 上有解,
上有解,
 ;
; ,
, ,
, ,
, =
= +
+ •
• >
> +
+ •
• =
= +
+ (
( ),
), >
> n+
n+ (
( +…+
+…+ -
- )=
)= n+
n+ =
= ,
,

科目:高中数学 来源:2012-2013学年浙江省温州市苍南中学高三(上)期中数学试卷(文科)(解析版) 题型:解答题
 (a为实常数).
(a为实常数). 上有解,求实数a的取值范围;
上有解,求实数a的取值范围; ,它的前n项和为Sn,求证:
,它的前n项和为Sn,求证: .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌二中高三(上)第二次月考数学试卷(文科)(解析版) 题型:解答题
 (a为实常数).
(a为实常数). .
.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省南昌三中高三(上)第三次月考数学试卷(理科)(解析版) 题型:解答题
 (a为实常数).
(a为实常数). .
.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省阜阳市颍上一中高考数学三模试卷(理科)(解析版) 题型:解答题
 (a为实常数).
(a为实常数). .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com