练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为响应“精确扶贫”号召，某企业计划每年用不超过100万元的资金购买单价分别为1500元/箱和3000元/箱的A、B两种药品捐献给贫困地区某医院，其中A药品至少100箱，B药品箱数不少于A药品箱数．则该企业捐献给医院的两种药品总箱数最多可为（ ）
    A.200
    B.350
    C.400
    D.500

    【答案】C
    【解析】解：设A药品为x箱，B药品为y箱，该企业捐献给医院的两种药品总箱数为z=x+y， 则x，y满足的关系式为 ，
    若x+y=500，又因为≥x，∴y≥250，
    则0.15x+0.3y=0.15（500﹣y）+0.3y=75+0.15y＞100，不合题意．
    若x+y=400，又因为y≥x，∴y≥200，
    则0.15x+0.3y=0.15（400﹣y）+0.3y=60+0.15y≥90，合题意．
    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知点P与两个定点O(0,0),A(-3,0)距离之比为.

    (1)求点P的轨迹C方程；

    (2)求过点M(2,3)且被轨迹C截得的线段长为2的直线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某知名品牌汽车深受消费者喜爱，但价格昂贵．某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车，并对近期100位采用上述分期付款的客户进行统计分析，得到如下的柱状图．已知从A、B、C三种分期付款销售中，该经销商每销售此品牌汽车1俩所获得的利润分别是1万元，2万元，3万元．现甲乙两人从该汽车经销商处，采用上述分期付款方式各购买此品牌汽车一辆．以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率．
    （1）求甲乙两人采用不同分期付款方式的概率；
    （2）记X（单位：万元）为该汽车经销商从甲乙两人购车中所获得的利润，求X的分布列与期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知sin（α+ ）= ，α∈（ ，π）．求：
    （1）cosα的值；
    （2）sin（2α﹣ ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= ，g（x）=lnx，其中e为自然对数的底数．
    （1）求函数y=f（x）g（x）在x=1处的切线方程；
    （2）若存在x1 ， x2（x1≠x2），使得g（x1）﹣g（x2）=λ[f（x2）﹣f（x1）]成立，其中λ为常数，求证：λ＞e；
    （3）若对任意的x∈（0，1]，不等式f（x）g（x）≤a（x﹣1）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校的平面示意图为如下图五边形区域ABCDE，其中三角形区域ABE为生活区，四边形区域BCDE为教学区，AB，BC，CD，DE，EA，BE为学校的主要道路（不考虑宽度）. ， ．
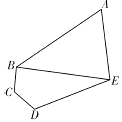
    （1）求道路BE的长度；
    （2）求生活区△ABE面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某程序框图如图所示，该程序运行后输出的S的值是（ ）
    A.3024
    B.1007
    C.2015
    D.2016

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ln（x+a）﹣x，a∈R．
    （1）当a=﹣1时，求f（x）的单调区间；
    （2）若x≥1时，不等式ef（x）+ x2＞1恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣2a|+|x+ |
    （1）当a=1时，求不等式f（x）＞4的解集；
    （2）若不等式f（x）≥m2﹣m+2 对任意实数x及a恒成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案