
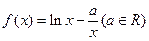 。
。 在定义域上的单调性;
在定义域上的单调性; 在
在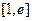 上的最小值为2,求
上的最小值为2,求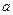 的值。
的值。 的定义域为
的定义域为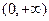 ,
,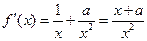 ……………………(2分)
……………………(2分)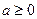 时,
时,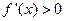 ,故
,故 在
在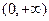 上为增函数…………………………(4分)
上为增函数…………………………(4分)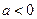 时,由
时,由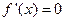 得
得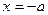 ;由
;由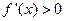 得
得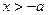 ;
;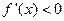 得
得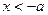 ;
; 在
在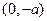 上为减函数;在
上为减函数;在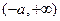 上为增函
上为增函 数.…………………………(6分)
数.…………………………(6分)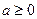 时,
时, 在
在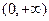 上是增函数;当
上是增函数;当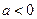 时,
时, 在
在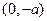 上是减函数,在
上是减函数,在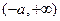 上是增函数…………………………………………………………………………(7分)
上是增函数…………………………………………………………………………(7分)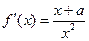 ,
,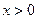 .由(1)可知:
.由(1)可知: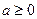 时,
时, 在
在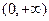 上为增函数,
上为增函数,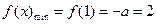 ,得
,得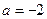 ,矛盾!
,矛盾!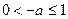 时,即
时,即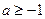 时,
时, 在
在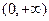 上也是增函数,
上也是增函数,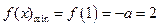 ,∴
,∴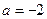 (舍去).………………………………………(9分)
(舍去).………………………………………(9分)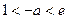 时,即
时,即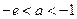 时,
时, 在
在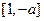 上是
上是 减函数,在
减函数,在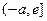 上是增函数,
上是增函数,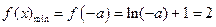 ,得
,得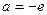 (舍去).………………………(10分)
(舍去).………………………(10分)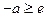 时,即
时,即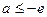 时,
时, 在
在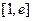 上是减函数,有
上是减函数,有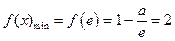 ,
,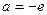 …………………………………………………………………………(11分)
…………………………………………………………………………(11分)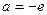 .……………………………………………………………………(12分)
.……………………………………………………………………(12分)

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:不详 题型:单选题
| A.a>b>c | B.c>b>a |
| C.c>a>b | D.a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com