
【题目】某程序框图如图所示,该程序运行后输出![]() 的值是( )
的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文、理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.

(1)求a的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,并判断能否有超过95%的把握认为“获奖与学生的文、理科有关”?
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
附表及公式: 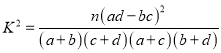
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
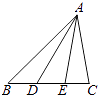
【题目】如图,D、E分别是△ABC的边BC的三等分点,设 ![]() =m,
=m, ![]() =n,∠BAC=
=n,∠BAC= ![]() .
. 
(1)用 ![]() 、
、 ![]() 分别表示
分别表示 ![]() ,
, ![]() ;
;
(2)若 ![]()
![]() =15,|
=15,| ![]() |=3
|=3 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=xlnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)对x≥1,f(x)≤m(x2﹣1)成立,求实数m的最小值;
(3)证明:1n ![]()
![]() .(n∈N*)
.(n∈N*)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍。为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* .
(1)证明:数列{ ![]() }是等差数列;
}是等差数列;
(2)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l. 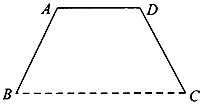
(1)请将l表示成关于α的函数l=f(α);
(2)问当α为何值时l最小?并求最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com