
【题目】如图,已知三棱柱![]() 的所有棱长均为2,
的所有棱长均为2,![]() .
.
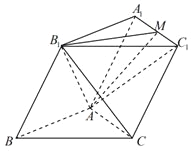
(Ⅰ)证明:![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的圆柱![]() 中,AB为圆
中,AB为圆![]() 的直径,
的直径,![]() 是
是![]() 的两个三等分点,EA,FC,GB都是圆柱
的两个三等分点,EA,FC,GB都是圆柱![]() 的母线.
的母线.
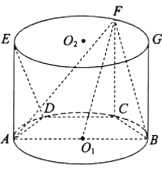
(1)求证:![]() 平面ADE;
平面ADE;
(2)设BC=1,已知直线AF与平面ACB所成的角为30°,求二面角A—FB—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
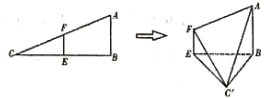
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆![]() ,圆
,圆![]() .
.
(1)证明:圆![]() 与圆
与圆![]() 有公共点,并求公共点的轨迹
有公共点,并求公共点的轨迹![]() 的方程;
的方程;
(2)已知点![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与(1)中轨迹
的直线与(1)中轨迹![]() 相交于
相交于![]() 两点,记直线
两点,记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
(1)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
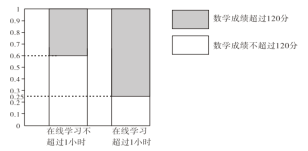
(2)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠州市某学校高三年级模拟考试的数学试题是全国I卷的题型结构,其中第22、23题为选做题,考生只需从中任选一题作答.已知文科数学和理科数学的选做题题目无任何差异,该校参加模拟考试学生共1050人,其中文科学生150人,理科学生900人.在测试结束后,数学老师对该学校全体高三学生选做的22题和23题得分情况进行了统计,22题统计结果如下表1,23题统计结果如下表2.
表1
22题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 70 | 80 | 100 | 500 |
文科人数 | 5 | 20 | 10 | 5 | 70 |
表2
23题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 10 | 10 | 15 | 25 | 40 |
文科人数 | 5 | 5 | 25 | 0 | 5 |
(1)在答卷中完成如下![]() 列联表,并判断能否至少有
列联表,并判断能否至少有![]() 的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
选做22题 | 选做23题 | 合计 | |
文科人数 | 110 | ||
理科人数 | 100 | ||
总计 | 1050 |
(2)在第23题得分为0的学生中,按分层抽样的方法随机抽取6人进行答疑辅导,并在辅导后从这6人中随机抽取2人进行测试,求被抽中进行测试的2名学生均为理科生的概率.
参考公式: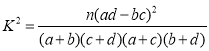 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上每一点到直线l:![]() 的距离比它到点
的距离比它到点![]() 的距离大1.
的距离大1.
(1)求曲线C的方程;
(2)曲线C任意一点处的切线m(不含x轴)与直线![]() 相交于点M,与直线l相交于点N,证明:
相交于点M,与直线l相交于点N,证明:![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com