
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下(提示:可以用第(2)问的结论),任意的![]() ,证明:
,证明:![]() .
.
【答案】(1)见解析;(2)![]() ;(3)见解析 .
;(3)见解析 .
【解析】
(1)确定函数![]() 的定义域,求
的定义域,求![]() ,对
,对![]() 分类讨论确定区间
分类讨论确定区间![]() 上
上![]() 的根的情况,从而确定函数
的根的情况,从而确定函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上恒成立,则只需函数
上恒成立,则只需函数![]() 即可,故根据第(1)问中函数
即可,故根据第(1)问中函数![]() 的单调性,可确定当
的单调性,可确定当![]() 时函数
时函数![]() 有最大值
有最大值![]() ,利用导数法可判断
,利用导数法可判断![]() ,进而可得
,进而可得![]() ,从而可求得
,从而可求得![]() 的范围;
的范围;
(3)![]() 可化为
可化为 ,结合由(2)得,
,结合由(2)得,![]() 时,
时,![]() ,而
,而![]() ,故可得
,故可得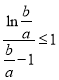 ,又
,又![]() ,进而可证得结果.
,进而可证得结果.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() .
.
①当![]() 时,
时,![]() 在
在![]() 上单调增
上单调增
②当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调增;
上单调增;
③当![]() 时,
时,
令![]() 得,
得,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
令![]() 得,
得,![]() ,所以
,所以![]() 在
在![]() 上单调递减.
上单调递减.
(2)由(1)知,当![]() 时,
时,![]() 在
在![]() 上单调增,且
上单调增,且![]() ,
,
所以![]() 在
在![]() 上不恒成立;
上不恒成立;
当![]() 时,由(1)知,
时,由(1)知,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,故只需
,故只需![]() 即可,
即可,
令![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() ,又
,又![]() ,
,
所以![]() ,解得
,解得![]()
综上,![]() 的取值范围是
的取值范围是![]() .
.
(3)注意:用第(2)题的结论:![]() 时,
时,![]() .
.
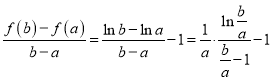 ,
,
因为![]() ,所以
,所以![]() ,由(2)得,
,由(2)得,![]() 时,
时,![]()
令![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即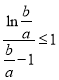 ,
,
因为![]() ,所以
,所以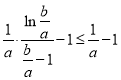 .
.


科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
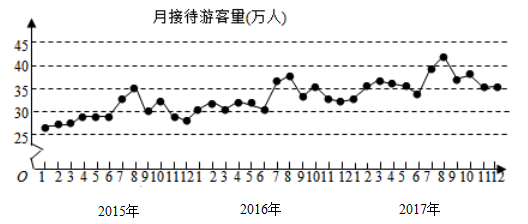
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市高中某学科竞赛中,某一个区4000名考生的参赛成绩统计如图所示.
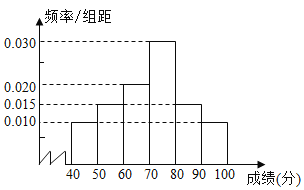
(1)求这4000名考生的竞赛平均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 720 |
|
|
女生 |
| 1020 |
|
合计 |
|
| 4000 |
附:
p(k2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
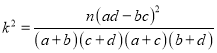 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省新高考将实行“![]() ”模式,“3”为全国统考科目语文数学外语,所有学生必考;“1”为首选科目,考生须在物理历史两科中选择一科;“2”为再选科目,考生可在化学生物思想政治地理4个科目中选择两科.某考生已经确定“首选科目”为物理,如果他从“再选科目”中随机选择两科,则思想政治被选中的概率为( )
”模式,“3”为全国统考科目语文数学外语,所有学生必考;“1”为首选科目,考生须在物理历史两科中选择一科;“2”为再选科目,考生可在化学生物思想政治地理4个科目中选择两科.某考生已经确定“首选科目”为物理,如果他从“再选科目”中随机选择两科,则思想政治被选中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() ,
,![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,且对任意的
,且对任意的![]() 都有
都有![]() ,已知
,已知![]() ,数列
,数列![]() 和
和![]() 是公差不为0的等差数列,且各项均为非负整数.
是公差不为0的等差数列,且各项均为非负整数.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() 的前4项删去1项后按原来顺序成等比数列,求所有满足条件的数列
的前4项删去1项后按原来顺序成等比数列,求所有满足条件的数列![]() ;
;
(3)若![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() ,
,![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=AA1.

(1)求证:AB1⊥平面A1BC1;
(2)若D在B1C1上,满足B1D=2DC1,求AD与平面A1BC1所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,函数
,函数![]() 与
与![]() 关于直线
关于直线![]() 对称.
对称.
(1)若函数![]() 在区间
在区间![]() 上递增,求a的取值范围;
上递增,求a的取值范围;
(2)证明:![]() ;
;
(3)设![]() ,其中
,其中![]() 恒成立,求满足条件的最小正整数b的值.
恒成立,求满足条件的最小正整数b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com