【题目】执行如图所示的程序框图，若输出
的值为4，则判断框中应填入的条件是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
根据程序框图，写出每一步的运行结果，由对数函数换底公式计算得到每一步的最后结果，最后由程序输出的结果是S＝4，可得判断框内应填入的条件．
解：根据程序框图，运行结果如下：
第一次循环 s=log23 k=3
第二次循环 s=log23log34=
k=4
第三次循环 s=log23log34log45=
k=5
第四次循环 s=log23log34log45log56=
k=6
第五次循环 s=log23log34log45log56log67=
k=7
第六次循环 s=log23log34log45log56log67log78=
k=8
第七次循环 s=log23log34log45log56log67log78log89=
k=9
…
第十三次循s=log23log34log45log56…log1415=
k=15
第十四次循环 s=log23log34log45log56…log1415log1516＝log216＝4 k=16
故如果输出S＝4，那么只能进行十四次循环，故判断框内应填入的条件是k＜16．
故选：C．
科目：高中数学 来源： 题型：
【题目】如图，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的，G是
的中点.
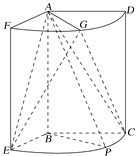
(1)设P是
上的一点，且AP⊥BE，求∠CBP的大小；
(2)当AB＝3，AD＝2时，求二面角E－AG－C的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】利用独立性检验的方法调查高中生性别与爱好某项运动是否有关，通过随机调查200名高中生是否爱好某项运动，利用
列联表，由计算可得
，参照下表：
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5,024 | 6.635 | 7.879 | 10.828 |
得到的正确结论是（ ）
A. 有99%以上的把握认为“爱好该项运动与性别无关”
B. 有99%以上的把握认为“爱好该项运动与性别有关”
C. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.5%的前提下，认为“爱好该项运动与性别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
、
为抛物线
上的两点，与的中点的纵坐标为4，直线
的斜率为
.
（1）求抛物线
的方程；
（2）已知点
，
、
为抛物线（除原点外）上的不同两点，直线
、
的斜率分别为
，
，且满足
，记抛物线在、处的切线交于点
，若点、的中点的纵坐标为8，求点
的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某省级示范高中高三年级对考试的评价指标中，有“难度系数”和“区分度”两个指标.其中，难度系数=年级总平均分
总分，区分度=（实验班的平均分—普通班的平均分）总分.
（1）某次数学考试满分150分，随机从实验班和普通班各抽取三人，实验班三人的成绩分别为：147、142、137；普通班三人的成绩分别为：97、102、113，通过样本计算本次考试的区分度（精确到0.01）；
（2）以下表格是高三年级6次考试的统计数据：
令
，求出
关于
的线性回归方程，并预报
时的值（系数精确到0.01）.
参考数据：
，
.
回归方程中斜率和截距的最小二乘法公式分别为：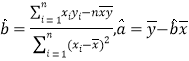
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司拟设计一个扇环形状的花坛（如图所示），该扇环是由以点
为圆心的两个同心圆弧和延长后通过点
的两条线段围成．设圆弧
、
所在圆的半径分别为
、
米，圆心角为
（弧度）．
（1）若
，
，
，求花坛的面积；
（2）设计时需要考虑花坛边缘（实线部分）的装饰问题，已知直线部分的装饰费用为
元/米，弧线部分的装饰费用为
元/米，预算费用总计
元，问线段的长度为多少时，花坛的面积最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
