Question

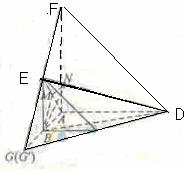
（四川卷理19）如，平面平面，

四边形与都是直角梯形，

，

（Ⅰ）证明：四点共面；

（Ⅱ）设，求二面角的大小；

Answer 1

【解1】：（Ⅰ）延长交的延长线于点，由得

        

延长交的延长线于

同理可得 

故，即与重合

因此直线相交于点，即四点共面。

（Ⅱ）设，则，

取中点，则，又由已知得，平面

故，与平面内两相交直线都垂直。

所以平面，作，垂足为，连结

由三垂线定理知为二面角的平面角。

　　　

故所以二面角的大小

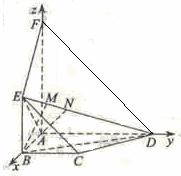
【解2】：由平面平面，，得平面，以为坐标原点，射线为轴正半轴，建立如图所示的直角坐标系

（Ⅰ）设，则

　　

故，从而由点，得

故四点共面

（Ⅱ）设，则，

在上取点，使，则

从而

又

在上取点，使，则

从而

故与的夹角等于二面角的平面角，　　，所以二面角的大小

【点评】：此题重点考察立体几何中四点共面问题和求二面角的问题，考察空间想象能力，几何逻辑推理能力，以及计算能力；

【突破】：熟悉几何公理化体系，准确推理，注意书写格式是顺利进行解法1的关键；在解法2中，准确的建系，确定点坐标，熟悉向量的坐标表示，熟悉空间向量的计算在几何位置的证明，在有关线段，角的计算中的计算方法是解题的关键。