
分析 通过f(-1)=-2,推出a,b的关系,利用不等式f(x)≥2x对一切x∈R都成立,转化为判别式△≤0,进行求解即可.
解答 解:∵f(x)=x2+(lga+2)x+lgb,且f(-1)=-2,
∴f(-1)=1-(lga+2)+lgb=-2,
即lga-lgb=1,
即lg$\frac{a}{b}$=1,则$\frac{a}{b}$=10,即lga=1+lgb,
则f(x)=x2+(3+lgb)x+lgb,
若f(x)≥2x对一切x∈R都成立,
即x2+(3+lgb)x+lgb≥2x,对一切x∈R都成立,
即x2+(1+lgb)x+lgb≥0恒成立,
则判别式△=(1+lgb)2-4lgb≤0,
即(1-lgb)2≤0,
则1-lgb=0,即lgb=1,则b=10,a=10b=100,
则a+b=10+100=110,
点评 本题主要考查不等式恒成立问题,根据条件求出a,b的关系,以及利用不等式恒成立转化为一元二次不等式与判别式△的关系是解决本题的关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
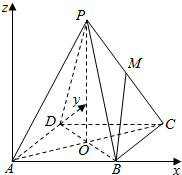 如图,在正四棱锥P-ABCD中,底面ABCD是边长为1的正方形,O是AC与BD的交点,PO=1,M是PC的中点.
如图,在正四棱锥P-ABCD中,底面ABCD是边长为1的正方形,O是AC与BD的交点,PO=1,M是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$π | B. | $\frac{\sqrt{3}}{2}$π | C. | $\frac{7\sqrt{7}}{6}$π | D. | $\frac{7\sqrt{7}}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com