
【题目】如图,在三棱柱![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.
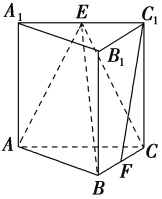
(1)求证:![]() 平面
平面![]() ;
;
(2)过点![]() 作一个截面
作一个截面![]() ,使平面
,使平面![]() 平面
平面![]() ,并证明.
,并证明.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在同一个平面内,向量 ![]() ,
, ![]() ,
, ![]() 的模分别为1,1,
的模分别为1,1, ![]() ,
, ![]() 与
与 ![]() 的夹角为α,且tanα=7,
的夹角为α,且tanα=7, ![]() 与
与 ![]() 的夹角为45°.若
的夹角为45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),则m+n= .
(m,n∈R),则m+n= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆的中心在原点,焦点在![]() 轴上,点
轴上,点![]() 是椭圆上的一点,
是椭圆上的一点,![]() 在
在![]() 轴上的射影恰为椭圆的左焦点,
轴上的射影恰为椭圆的左焦点,![]() 与中心
与中心![]() 的连线平行于右顶点与上顶点的连线,且左焦点与左顶点的距离等于
的连线平行于右顶点与上顶点的连线,且左焦点与左顶点的距离等于![]() ,试求椭圆的离心率及其方程.
,试求椭圆的离心率及其方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(10分)
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种设备的单价为![]() 元,设备维修和消耗费用第一年为
元,设备维修和消耗费用第一年为![]() 元,以后每年增加
元,以后每年增加![]() 元(
元(![]() 是常数).用
是常数).用![]() 表示设备使用的年数,记设备年平均费用为
表示设备使用的年数,记设备年平均费用为![]() ,即
,即![]() (设备单价
(设备单价![]() 设备维修和消耗费用)
设备维修和消耗费用)![]() 设备使用的年数.
设备使用的年数.
(Ⅰ)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)当![]() ,
, ![]() 时,求这种设备的最佳更新年限.
时,求这种设备的最佳更新年限.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,
中,![]() 在直线
在直线![]() .
.
(1)求数列{an}的通项公式;
(2)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整数λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B为曲线C:y= ![]() 上两点,A与B的横坐标之和为4.(12分)
上两点,A与B的横坐标之和为4.(12分)
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin(ωx﹣
sin(ωx﹣ ![]() )+b(ω>0),且函数图象的对称中心到对称轴的最小距离为
)+b(ω>0),且函数图象的对称中心到对称轴的最小距离为 ![]() ,当x∈[0,
,当x∈[0, ![]() ]时,f(x)的最大值为1.
]时,f(x)的最大值为1.
(1)求函数f(x)的解析式;
(2)将函数f(x)的图象向右平移 ![]() 个单位长度得到函数g(x)图象,若g(x)﹣3≤m≤g(x)+3在x∈[0,
个单位长度得到函数g(x)图象,若g(x)﹣3≤m≤g(x)+3在x∈[0, ![]() ]上恒成立,求实数m的取值范围.
]上恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com