【答案】
分析:①根据偶函数f(x)在[0,3]上为增函数,则f(x)在[-3,0]上是减函数,知①不正确;
②将f(3)=0代入,得到f(x+6)=f(x),故f(x)是周期等于6的周期函数,再由f(x)是偶函数可得,x=-6是函数y=f(x)的图象的一条对称轴;
③令x=-3,代入f(x+6)=f(x)+f(3),根据函数为偶函数,得到f(3)=0;
④根据f(3)=0,周期为6,得到f(-9)=f(-3)=f(3)=f(9)=0,有四个零点.
解答:解:①因为当x
1,x
2∈[0,3],x
1≠x
2时,有

>0 成立,故f(x)在[0,3]上为增函数,
又f(x)为偶函数,故在[-3,0]上为减函数,故①错误;
②令x=-3,由f(x+6)=f(x)+f(3),得f(3)=f(-3)+f(3),
∵y=f (x)在R上是偶函数,∴f(3)=0,
∴f(x+6)=f(x),故f(x)是周期等于6的周期函数.
由于f(x)为偶函数,y轴是对称轴,
故直线x=-6也是函数y=f(x)的图象的一条对称轴,故②正确.
③令x=-3,则由f(x+6)=f(x)+f(3),函数y=f (x)在R上是偶函数,
得f(3)=f(-3)+f(3)=2f(3),故f(3)=0,故③正确.
④函数f(x)周期为6,故f(-9)=f(-3)=f(3)=f(9)=0,
故y=f(x)在[-9,9]上有四个零点,故④正确.
故答案为:②③④.
点评:本题考查了抽象函数的单调性,奇偶性,周期性,综合性比较强,需熟练灵活掌握,属于基础题.

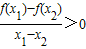 ,给出如下命题:
,给出如下命题: >0 成立,故f(x)在[0,3]上为增函数,
>0 成立,故f(x)在[0,3]上为增函数,

 阅读快车系列答案
阅读快车系列答案 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为