
分析 先由题意先求[x],再求x[x],然后再求[x[x]],得到an,进而得到$\frac{{a}_{n}+90}{n}$,用基本不等式求解.
解答 解:根据题意:[x]=$\left\{\begin{array}{l}0,x∈[0,1)\\ 1,x∈[1,2)\\ 2,x∈[2,3)\\…\\ n-1,x∈[n-1,n)\end{array}\right.$,
∴x[x]=$\left\{\begin{array}{l}0,x∈[0,1)\\ x,x∈[1,2)\\ 2x,x∈[2,3)\\…\\(n-1)x,x∈[n-1,n)\end{array}\right.$,
∴[x[x]]在各区间中的元素个数是:1,1,2,3,…,n-1
∴an=$\frac{n(n-1)}{2}$+1,
∴a3=4,
∴$\frac{{a}_{n}+90}{n}$=$\frac{1}{2}$(n+$\frac{180}{n}$-1),所以当n=13或14时,最小值为13.
故答案为:4,13.
点评 本题主要通过取整函数来建立新函数,进而研究其定义域和值域.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
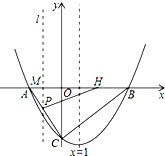 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com