
关于 的不等式
的不等式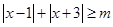 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是 .
的取值范围是 .
科目:高中数学 来源:2008届宁夏省中卫一中高三第二学期第一次模拟、理科数学 题型:044
定义在R上的函数f(x)=ax3+bx2+cx+d(a,b,c,d∈R),当x=-1时,f(x)取得极值![]() 且函数y=f(x)的图像关于原点成中心对称,g(x)=-mx-4.
且函数y=f(x)的图像关于原点成中心对称,g(x)=-mx-4.
(1)求f(x)的解析式;
(2)若不等式![]() 恒成立,求实数m的取值范围
恒成立,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)f(x)≤0在区间[-1,1]上恒成立时,求实数a的值组成的集合A;
(2)设关于x的方程f(x)=0的两个实根为x1,x2,求证:对任意a∈A,b∈A,不等式g(x)≥|x1-x2|恒成立.
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高一第二学期第一次月考数学试 题型:填空题
三个同学对问题“关于 的不等式
的不等式 +25+|
+25+| -5
-5 |≥
|≥ 在[1,12]上恒成
在[1,12]上恒成
立,求实数 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量 的函数,右边仅含常数,求函数的最值”.
的函数,右边仅含常数,求函数的最值”.
丙说:“把不等式两边看成关于 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com