
ЁОЬтФПЁП2020Фъ1дТ10ШеЃЌв§ЗЂаТЙкЗЮбзвпЧщЕФCOVID-9ВЁЖОЛљвђађСаЙЋВМКѓЃЌПЦбЇМвУЧБуПЊЪМСЫВЁЖОвпУчЕФбаОПЙ§ГЬ.ЕЋЪЧРрЫЦетжжВЁЖОвпУчЕФбажЦашвЊПЦбЇЕФСїГЬЃЌВЛЪЧвЛГЏвЛЯІФмЭъГЩЕФЃЌЦфжагавЛВНОЭЪЧзіЖЏЮяЪдбщ.вбжЊвЛИіПЦбаЭХЖггУаЁАзЪѓзіНгжжЪдбщЃЌМьВтНгжжвпУчКѓЪЧЗёГіЯжПЙЬх.ЪдбщЩшМЦЪЧЃКУПЬьНгжжвЛДЮЃЌ3ЬьЮЊвЛИіНгжжжмЦк.вбжЊаЁАзЪѓНгжжКѓЕБЬьГіЯжПЙЬхЕФИХТЪЮЊ![]() ЃЌМйЩшУПДЮНгжжКѓЕБЬьЪЧЗёГіЯжПЙЬхгыЩЯДЮНгжжЮоЙи.
ЃЌМйЩшУПДЮНгжжКѓЕБЬьЪЧЗёГіЯжПЙЬхгыЩЯДЮНгжжЮоЙи.
ЃЈ1ЃЉЧѓвЛИіНгжжжмЦкФкГіЯжПЙЬхДЮЪ§![]() ЕФЗжВМСаЃЛ
ЕФЗжВМСаЃЛ
ЃЈ2ЃЉвбжЊУПЬьНгжжвЛДЮЛЈЗб100дЊЃЌЯжгавдЯТСНжжЪдбщЗНАИЃК
ЂйШєдквЛИіНгжжжмЦкФкСЌај2ДЮГіЯжПЙЬхМДжежЙБОжмЦкЪдбщЃЌНјааЯТвЛНгжжжмЦкЃЌЪдбщГжајШ§ИіНгжжжмЦкЃЌЩшДЫжжЪдбщЗНЪНЕФЛЈЗбЮЊ![]() дЊЃЛ
дЊЃЛ
ЂкШєдквЛИіНгжжжмЦкФкГіЯж2ДЮЛђ3ДЮПЙЬхЃЌИУжмЦкНсЪјКѓжежЙЪдбщЃЌвбжЊЪдбщжСЖрГжајШ§ИіНгжжжмЦкЃЌЩшДЫжжЪдбщЗНЪНЕФЛЈЗбЮЊ![]() дЊ.
дЊ.
БШНЯЫцЛњБфСП![]() КЭ
КЭ![]() ЕФЪ§бЇЦкЭћЕФДѓаЁ.
ЕФЪ§бЇЦкЭћЕФДѓаЁ.
ЁОД№АИЁПЃЈ1ЃЉЗжВМСаД№АИМћНтЮі.ЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩжЊЃЌЫцЛњБфСП![]() ЗўДгЖўЯюЗжВМ
ЗўДгЖўЯюЗжВМ![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌШЛКѓСаГіЗжВМСаМДПЩ
ЃЌШЛКѓСаГіЗжВМСаМДПЩ
ЃЈ2ЃЉИљОнЬтвтЗжБ№ЫуГі![]() КЭ
КЭ![]() ЕФЦкЭћМДПЩ.
ЕФЦкЭћМДПЩ.
ЃЈ1ЃЉгЩЬтвтПЩжЊЃЌЫцЛњБфСП![]() ЗўДгЖўЯюЗжВМ
ЗўДгЖўЯюЗжВМ![]() ЃЌ
ЃЌ
ЙЪ![]() .
.
дђ![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
ЃЈ2ЃЉЂйЩшвЛИіНгжжжмЦкЕФНгжжЗбгУЮЊ![]() дЊЃЌдђ
дЊЃЌдђ![]() ПЩФмЕФШЁжЕЮЊ200ЃЌ300ЃЌ
ПЩФмЕФШЁжЕЮЊ200ЃЌ300ЃЌ
вђЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ыљвд![]() .
.
ЫљвдШ§ИіНгжжжмЦкЕФЦНОљЛЈЗбЮЊ![]() .
.
ЂкЫцЛњБфСП![]() ПЩФмЕФШЁжЕЮЊ300ЃЌ600ЃЌ900ЃЌ
ПЩФмЕФШЁжЕЮЊ300ЃЌ600ЃЌ900ЃЌ
ЩшЪТМў![]() ЮЊЁАдквЛИіНгжжжмЦкФкГіЯж2ДЮЛђ3ДЮПЙЬхЁБЃЌгЩЃЈ1ЃЉжЊЃЌ
ЮЊЁАдквЛИіНгжжжмЦкФкГіЯж2ДЮЛђ3ДЮПЙЬхЁБЃЌгЩЃЈ1ЃЉжЊЃЌ![]() .
.
Ыљвд![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ыљвд![]() .
.
Ыљвд![]() .
.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬте§ШЗЕФЪЧЃЈ ЃЉ
A.вбжЊЫцЛњБфСП![]() ЃЌШє
ЃЌШє![]() .дђ
.дђ![]()
B.вбжЊЗжРрБфСП![]() гы
гы![]() ЕФЫцЛњБфСП
ЕФЫцЛњБфСП![]() ЕФЙлВьжЕЮЊ
ЕФЙлВьжЕЮЊ![]() ЃЌдђЕБ
ЃЌдђЕБ![]() ЕФжЕдНДѓЪБЃЌЁА
ЕФжЕдНДѓЪБЃЌЁА![]() гы
гы![]() гаЙиЁБЕФПЩаХЖШдНаЁ.
гаЙиЁБЕФПЩаХЖШдНаЁ.
C.дкЯпадЛиЙщФЃаЭжаЃЌМЦЫуЦфЯрЙижИЪ§![]() ЃЌдђПЩвдРэНтЮЊЃКНтЮіБфСПЖддЄБЈБфСПЕФЙБЯзТЪдМЮЊ
ЃЌдђПЩвдРэНтЮЊЃКНтЮіБфСПЖддЄБЈБфСПЕФЙБЯзТЪдМЮЊ![]()
D.ШєЖдгкБфСП![]() гы
гы![]() ЕФ
ЕФ![]() зщЭГМЦЪ§ОнЕФЯпадЛиЙщФЃаЭжаЃЌЯрЙижИЪ§
зщЭГМЦЪ§ОнЕФЯпадЛиЙщФЃаЭжаЃЌЯрЙижИЪ§![]() .гжжЊВаВюЦНЗНКЭЮЊ
.гжжЊВаВюЦНЗНКЭЮЊ![]() .ФЧУД
.ФЧУД![]() .ЃЈзЂвтЃК
.ЃЈзЂвтЃК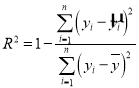 ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЖЗЙАЁБЪЧжаЙњЙХДњНЈжўжаЬигаЕФЙЙМўЃЌДгзюГѕЕФГажизїгУЃЌЕНУїЧхЪБЦкМЏГажигызАЪЮзїгУгквЛЬхЁЃдкСЂжљЖЅЁЂЖюшЪКЭщмщнМфЛђЙЙМмМфЃЌДгшЪЩЯМгЕФвЛВуВуЬНГіГЩЙаЮЕФГажиНсЙЙНаЙАЃЌЙАгыЙАжЎМфЕцЕФЗНаЮФОПщНаЖЗЁЃШчЭМЫљЪОЃЌЪЧЁАЩЂЖЗЁБЃЈгжУћЁАШ§ВХЩ§ЁБЃЉЕФШ§ЪгЭМЃЌдђЫќЕФЬхЛ§ЮЊЃЈ ЃЉ

A. ![]() B.
B. ![]() C. 53 D.
C. 53 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЃЌШє
ЃЌШє![]() ЃЌдђ
ЃЌдђ![]() ЕФзюаЁжЕЮЊ__________ЃЛШє
ЕФзюаЁжЕЮЊ__________ЃЛШє![]() ЃЌдђ
ЃЌдђ![]() ЕФзюДѓжЕЮЊ__________ЃЎ
ЕФзюДѓжЕЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПДѓаЭзлвеНкФПЁЖзюЧПДѓФдЁЗжаЃЌгавЛИігЮЯЗНазіУЄХЁФЇЗНЃЌОЭЪЧЭцМвЯШЙлВьФЇЗНзДЬЌВЂНјааМЧвфЃЌМЧзЁКѓУЩзЁблОІПьЫйЛЙдФЇЗНЃЌУЄХЁдкЭтШЫПДРДКмЩёЦцЃЌЦфЪЕдРэЪЧЪЎЗжМђЕЅЕФЃЌвЊбЇЛсУЄХЁвВЪЧКмШнвзЕФ.ЮЊСЫНтФГЪаУЄХЁФЇЗНАЎКУепЕФЫЎЦНзДПіЃЌФГаЫШЄаЁзщдкШЋЪаЗЖЮЇФкЫцЛњГщШЁСЫ![]() УћФЇЗНАЎКУепНјааЕїВщЃЌЕУЕНЕФЧщПіШчБэЫљЪОЃК
УћФЇЗНАЎКУепНјааЕїВщЃЌЕУЕНЕФЧщПіШчБэЫљЪОЃК
гУЪБЃЈУыЃЉ |
|
|
|
|
ФаадШЫЪ§ | 15 | 22 | 14 | 9 |
ХЎадШЫЪ§ | 5 | 11 | 17 | 7 |
ИНЃК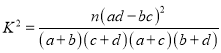 ЃЌ
ЃЌ![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
ЃЈ1ЃЉНЋгУЪБЕЭгк![]() УыЕФГЦЮЊЁАЪьСЗУЄХЁепЁБЃЌВЛЕЭгк
УыЕФГЦЮЊЁАЪьСЗУЄХЁепЁБЃЌВЛЕЭгк![]() УыЕФГЦЮЊЁАЗЧЪьСЗУЄХЁепЁБ.ЧыИљОнЕїВщЪ§ОнЭъГЩвдЯТ
УыЕФГЦЮЊЁАЗЧЪьСЗУЄХЁепЁБ.ЧыИљОнЕїВщЪ§ОнЭъГЩвдЯТ![]() СаСЊБэЃЌВЂХаЖЯЪЧЗёга
СаСЊБэЃЌВЂХаЖЯЪЧЗёга![]() ЕФАбЮеШЯЮЊЪЧЗёЮЊЁАЪьСЗУЄХЁепЁБгыадБ№гаЙиЃП
ЕФАбЮеШЯЮЊЪЧЗёЮЊЁАЪьСЗУЄХЁепЁБгыадБ№гаЙиЃП
ЪьСЗУЄХЁеп | ЗЧЪьСЗУЄХЁеп | |
Фаад | ||
ХЎад |
ЃЈ2ЃЉвдет![]() УћУЄХЁФЇЗНАЎКУепЕФгУЪБВЛГЌЙ§
УћУЄХЁФЇЗНАЎКУепЕФгУЪБВЛГЌЙ§![]() УыЕФЦЕТЪЃЌДњЬцШЋЪаЫљгаУЄХЁФЇЗНАЎКУепЕФгУЪБВЛГЌЙ§
УыЕФЦЕТЪЃЌДњЬцШЋЪаЫљгаУЄХЁФЇЗНАЎКУепЕФгУЪБВЛГЌЙ§![]() УыЕФИХТЪЃЌУПЮЛУЄХЁФЇЗНАЎКУепгУЪБЪЧЗёГЌЙ§
УыЕФИХТЪЃЌУПЮЛУЄХЁФЇЗНАЎКУепгУЪБЪЧЗёГЌЙ§![]() УыЯрЛЅЖРСЂ.ФЧУДдкИУаЫШЄаЁзщдкШЋЪаЗЖЮЇФкдйДЮЫцЛњГщШЁ
УыЯрЛЅЖРСЂ.ФЧУДдкИУаЫШЄаЁзщдкШЋЪаЗЖЮЇФкдйДЮЫцЛњГщШЁ![]() УћАЎКУепНјааВтЪдЃЌЦфжагУЪБВЛГЌЙ§
УћАЎКУепНјааВтЪдЃЌЦфжагУЪБВЛГЌЙ§![]() УыЕФШЫЪ§зюгаПЩФмЃЈМДИХТЪзюДѓЃЉЪЧЖрЩйЃП
УыЕФШЫЪ§зюгаПЩФмЃЈМДИХТЪзюДѓЃЉЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩњЮяаЁзщЮЊСЫбаОПЮТЖШЖдФГжжУИЕФЛюадЕФгАЯьНјааСЫвЛзщЪЕбщЃЌЕУЕНЕФЪЕбщЪ§ОнОећРэЕУЕНШчЯТЕФелЯпЭМЃК
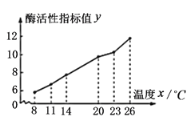
ЃЈ1ЃЉгЩЭМПЩвдПДГіЃЌетжжУИЕФЛюад![]() гыЮТЖШ
гыЮТЖШ![]() ОпгаНЯЧПЕФЯпадЯрЙиадЃЌЧыгУЯрЙиЯЕЪ§МгвдЫЕУїЃЛ
ОпгаНЯЧПЕФЯпадЯрЙиадЃЌЧыгУЯрЙиЯЕЪ§МгвдЫЕУїЃЛ
ЃЈ2ЃЉЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЌВЂдЄВтЕБЮТЖШЮЊ
ЕФЯпадЛиЙщЗНГЬЃЌВЂдЄВтЕБЮТЖШЮЊ![]() ЪБЃЌетжжУИЕФЛюаджИБъжЕ.ЃЈМЦЫуНсЙћОЋШЗЕН0.01ЃЉ
ЪБЃЌетжжУИЕФЛюаджИБъжЕ.ЃЈМЦЫуНсЙћОЋШЗЕН0.01ЃЉ
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ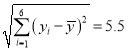 ЃЌ
ЃЌ![]() .
.
ВЮПМЙЋЪНЃКЯрЙиЯЕЪ§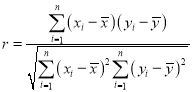 .
.
ЛиЙщжБЯпЗНГЬ![]() ЃЌ
ЃЌ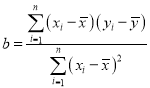 ЃЌ
ЃЌ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСагаЙиЯпадЛиЙщЗжЮіЕФЫФИіУќЬтЃК
ЂйЯпадЛиЙщжБЯпБиЙ§бљБОЪ§ОнЕФжааФЕуЃЈ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкЛиЙщжБЯпОЭЪЧЩЂЕуЭМжаОЙ§бљБОЪ§ОнЕузюЖрЕФФЧЬѕжБЯпЃЛ
ЂлЕБЯрЙиадЯЕЪ§![]() ЪБЃЌСНИіБфСПе§ЯрЙиЃЛ
ЪБЃЌСНИіБфСПе§ЯрЙиЃЛ
ЂмШчЙћСНИіБфСПЕФЯрЙиаддНЧПЃЌдђЯрЙиадЯЕЪ§![]() ОЭдННгНќгк
ОЭдННгНќгк![]() ЃЎ
ЃЎ
ЦфжаецУќЬтЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНЬхABCDЉA1B1C1D1ЕФРтГЄЮЊaЃЌЯпЖЮB1D1ЩЯгаСНИіЖЏЕуEЃЌFЃЌЧвEF![]() aЃЌвдЯТНсТле§ШЗЕФгаЃЈЁЁЁЁЃЉ
aЃЌвдЯТНсТле§ШЗЕФгаЃЈЁЁЁЁЃЉ

A.ACЁЭBE
B.ЕуAЕНЁїBEFЕФОрРыЮЊЖЈжЕ
C.Ш§РтзЖAЉBEFЕФЬхЛ§ЪЧе§ЗНЬхABCDЉA1B1C1D1ЬхЛ§ЕФ![]()
D.вьУцжБЯпAEЃЌBFЫљГЩЕФНЧЮЊЖЈжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЃК
ЃК![]() ЕФгвНЙЕу
ЕФгвНЙЕу![]() ЮЊХзЮяЯп
ЮЊХзЮяЯп![]() ЕФНЙЕуЃЌ
ЕФНЙЕуЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЭждВ
ЪЧЭждВ![]() ЩЯЕФСНИіЖЏЕуЃЌЧвЯпЖЮ
ЩЯЕФСНИіЖЏЕуЃЌЧвЯпЖЮ![]() ГЄЖШЕФзюДѓжЕЮЊ4.
ГЄЖШЕФзюДѓжЕЮЊ4.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() УцЛ§ЕФзюаЁжЕ.
УцЛ§ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com