
【题目】已知函数f(x)=|x﹣a|+m|x+a|.
(1)当m=a=﹣1时,求不等式f(x)≥x的解集;
(2)不等式f(x)≥2(0<m<1)恒成立时,实数a的取值范围是{a|a≤﹣3或a≥3},求实数m的集合.
【答案】
(1)解:m=a=﹣1时,|x+1|﹣|x﹣1|≥x,
x<﹣1时,﹣(x+1)+(x﹣1)≥x,解得:x≤﹣2,
﹣1≤x≤1时,(x+1)+(x﹣1)≥x,解得:0≤x<1,
x≥1时,(x+1)﹣(x﹣1)≥x,解得:1≤x≤2,
综上,不等式的解集是{x|x≤﹣2或0≤x≤2};
(2)解:f(x)=|x﹣a|+m|x+a|=m(|x﹣a|+|x+a|)+(1﹣m)|x﹣a|≥2m|a|+(1﹣m)|x﹣a|≥2m|a|≥2,
解得:a≤﹣ ![]() 或a≥
或a≥ ![]() ,
,
∵数a的取值范围是{a|a≤﹣3或a≥3},
故 ![]() =3,解得:m=
=3,解得:m= ![]() ,
,
∴实数m的集合是{m|m= ![]() }
}
【解析】(1)将m=a=﹣1代入(x),通过讨论x的范围求出不等式的解集即可;(2)根据绝对值的性质得到2m|a|≥2,解出a,得到关于m的方程,解出即可.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C1的极坐标方程为ρ=2sinθ,正方形ABCD的顶点都在C1上,且依次按逆时针方向排列,点A的极坐标为( ![]() ,
, ![]() ).
).
(1)求点C的直角坐标;
(2)若点P在曲线C2:x2+y2=4上运动,求|PB|2+|PC|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱锥P﹣ABCD中,底面ABCD的边长为4,PD=4,E为PA的中点, 
(1)求证:平面EBD⊥平面PAC;
(2)求直线BE与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲罐中有![]() 个红球,
个红球,![]() 个白球和
个白球和![]() 个黑球,乙罐中有
个黑球,乙罐中有![]() 个红球,
个红球,![]() 个白球和
个白球和![]() 个黑球。先从甲罐中随机取出一球放入乙罐,分别以
个黑球。先从甲罐中随机取出一球放入乙罐,分别以![]() 和
和![]() 表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以
表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以![]() 表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
表示由乙罐取出的球是红球的事件,则下列结论中正确的是________(写出所有正确结论的编号)。
①![]() ; ② 事件
; ② 事件![]() 与事件
与事件![]() 相互独立;③
相互独立;③![]()
④![]() 是两两互斥的事件;
是两两互斥的事件;
⑤![]() 的值不能确定,因为它与
的值不能确定,因为它与![]() 中哪一个发生有关
中哪一个发生有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a≠0),满足f(0)=2,f(x+1)﹣f(x)=2x﹣1
(1)求函数f(x)的解析式;
(2)当x∈[﹣1,2]时,求函数的最大值和最小值.
(3)若函数g(x)=f(x)﹣mx的两个零点分别在区间(﹣1,2)和(2,4)内,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个水轮的半径为4米,水轮圆心![]() 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点
距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点![]() 从水中浮现(图中点
从水中浮现(图中点![]() )开始计算时间.
)开始计算时间.
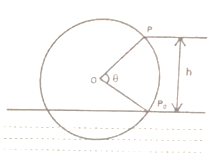
(1)将点![]() 距离水面的高度
距离水面的高度![]() (米)表示为时间
(米)表示为时间![]() (秒)的函数;
(秒)的函数;
(2)在水轮旋转一圈内,有多长时间点![]() 离开水面?
离开水面?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() (图1)的三视图如图2所示,
(图1)的三视图如图2所示,![]() 为正三角形,
为正三角形,![]() 垂直底面
垂直底面![]() ,俯视图是直角梯形.
,俯视图是直角梯形.


图1 图2
(1)求正视图的面积;
(2)求四棱锥![]() 的体积;
的体积;
(3)求证:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的参数方程为 ![]() (为参数,且0≤<2π),曲线l的极坐标方程为ρ=
(为参数,且0≤<2π),曲线l的极坐标方程为ρ= ![]() (k是常数,且k∈R).
(k是常数,且k∈R).
(1)求曲线C的普通方程和曲线l直角坐标方程;
(2)若曲线l被曲线C截的弦是以( ![]() ,1)为中点,求k的值.
,1)为中点,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com