
【题目】已知A、B、C是单位圆上三个互不相同的点.若 ![]() ,则
,则 ![]() 的最小值是( )
的最小值是( )
A.0
B.- ![]()
C.- ![]()
D.- ![]()
【答案】C
【解析】解:由题意可得,点A在BC的垂直平分线上,不妨设单位圆
的圆心为O(0,0),
点A(0,1),点B(x1 , y1),则点C(﹣x1 , y1),
﹣1≤y1<1.
∴ ![]() =(x1 , y1﹣1),
=(x1 , y1﹣1), ![]() =(﹣x1 , y1﹣1),
=(﹣x1 , y1﹣1), ![]() +
+ ![]() =1.
=1.
∴ ![]() =﹣
=﹣ ![]() +
+ ![]() ﹣2y1+1=﹣(1﹣
﹣2y1+1=﹣(1﹣ ![]() )+
)+ ![]() ﹣2y1+1
﹣2y1+1
=2 ![]() ﹣2y1 ,
﹣2y1 ,
∴当y1= ![]() 时,
时, ![]() 取得最小值为﹣
取得最小值为﹣ ![]() ,
,
故选:C.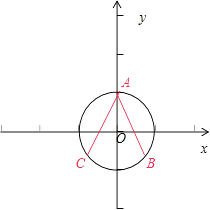
由题意可得,点A在BC的垂直平分线上,不妨设单位圆的圆心为O(0,0),点A(0,1),点B(x1 , y1),则点C(﹣x1 , y1), ![]() +
+ ![]() =1,且﹣1≤y1<1.根据
=1,且﹣1≤y1<1.根据 ![]() =2
=2 ![]() ﹣2y1 , 再利用二次函数的性质求得它的最小值.
﹣2y1 , 再利用二次函数的性质求得它的最小值.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点. 
(1)求证:PA∥平面EDB;
(2)求锐二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绿色出行越来越受到社会的关注,越来越多的消费者对新能源汽车感兴趣![]() 但是消费者比较关心的问题是汽车的续驶里程
但是消费者比较关心的问题是汽车的续驶里程![]() 某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程
某研究小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程![]() 单次充电后能行驶的最大里程
单次充电后能行驶的最大里程![]() ,被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:
,被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组: ![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
![]() 求直方图中m的值;
求直方图中m的值;
![]() 求本次调查中续驶里程在
求本次调查中续驶里程在![]() 的车辆数;
的车辆数;
![]() 若从续驶里程在
若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车续驶里程在![]() 的概率.
的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分![]() 分)已知圆
分)已知圆![]() 有以下性质:
有以下性质:
①过圆![]() 上一点
上一点![]() 的圆的切线方程是
的圆的切线方程是![]() .
.
②若![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
③若不在坐标轴上的点![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则
,则![]() 垂直
垂直![]() ,即
,即![]() ,且
,且![]() 平分线段
平分线段![]() .
.
(1)类比上述有关结论,猜想过椭圆![]() 上一点
上一点![]() 的切线方程(不要求证明);
的切线方程(不要求证明);
(2)过椭圆![]() 外一点
外一点![]() 作两直线,与椭圆相切于
作两直线,与椭圆相切于![]() 两点,求过
两点,求过![]() 两点的直线方程;
两点的直线方程;
(3)若过椭圆![]() 外一点
外一点![]() (
(![]() 不在坐标轴上)作两直线,与椭圆相切于
不在坐标轴上)作两直线,与椭圆相切于![]() 两点,求证:
两点,求证:![]() 为定值,且
为定值,且![]() 平分线段
平分线段![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在
的圆心在![]() 轴上,点
轴上,点![]() 是圆
是圆![]() 的上任一点,且当点
的上任一点,且当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 到直线
到直线![]() 距离最大.
距离最大.
(1)求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(2)已知![]() ,经过原点,且斜率为
,经过原点,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)求证:![]() 为定值;
为定值;
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com