
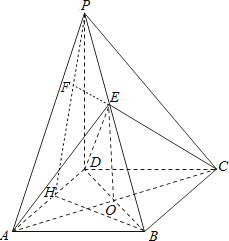
【题目】如图所示,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() ,
, ![]() .
. ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为棱
为棱![]() 上一点,
上一点,
(1)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,
,
求证: ![]() ∥平面
∥平面![]() .
.

【答案】(1)见解析 (2) 见解析
【解析】试题分析:(1)要证明平面![]() ⊥平面
⊥平面![]() ,由面面垂直的判定定理知需在平面
,由面面垂直的判定定理知需在平面![]() 平面
平面![]() 内找到一条直线垂直于另一个平面,通过分析后易知AC⊥平面PBD,再由线面垂直的判定定理即可证明.(2)由VP﹣EAD
内找到一条直线垂直于另一个平面,通过分析后易知AC⊥平面PBD,再由线面垂直的判定定理即可证明.(2)由VP﹣EAD![]() ,需作出三棱锥
,需作出三棱锥![]() 的高,为此通过观察分析后,我们取AD中点H,连结BH,PH,在△PBH中,经点E作EF∥BH,交PH于点F,易证BH⊥平面PAD,再由EF∥BH,可得EF⊥平面PAD,故EF为三棱锥
的高,为此通过观察分析后,我们取AD中点H,连结BH,PH,在△PBH中,经点E作EF∥BH,交PH于点F,易证BH⊥平面PAD,再由EF∥BH,可得EF⊥平面PAD,故EF为三棱锥![]() 的高,
的高,
再由VP﹣EAD![]() ,可求出EF的值,又由∠BAD=60°,BH⊥AD,可求出BH的值,至此易知
,可求出EF的值,又由∠BAD=60°,BH⊥AD,可求出BH的值,至此易知![]() ,即E为PB中点,而O为BD中点,所以OE为△PBD的中位线,由三角形中位线性质可得OE∥PD,再由线面平行判定定理PD∥平面EAC.
,即E为PB中点,而O为BD中点,所以OE为△PBD的中位线,由三角形中位线性质可得OE∥PD,再由线面平行判定定理PD∥平面EAC.
试题解析:
证明:(1)∵ABCD是菱形,∴AC⊥BD,
∵PD⊥底面ABCD,∴AC⊥PD,
∴AC⊥平面PBD,
又∵AC平面AEC,
∴平面AEC⊥平面PDB.
(2)取AD中点H,连结BH,PH,在△PBH中,经点E作EF∥BH,交PH于点F,
∵四边形ABCD是菱形,∠BAD=60°,
∴BH⊥AD,又BH⊥PD,AD∩PD=D,
∴BH⊥平面PAD,EF⊥平面PAD,
可得:BH=![]() AB=
AB=![]() ,
,
∴VP﹣EAD=VE﹣PAD=![]() SPAD×EF=
SPAD×EF= ![]()
![]() ,
,
∴EF=![]() ,
,
∴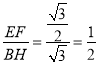 ,可得E为PB中点,
,可得E为PB中点,
又∵O为BD中点,
∴OE∥PD,
∵PD平面EAC,OE平面EAC,
∴PD∥平面EAC.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣2x , g(x)=lg(ax2﹣2x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
A.(﹣1,0)
B.(0,1)
C.(﹣∞,1]
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ) 当a=0时,求曲线f(x)在x =1处的切线方程;
(Ⅱ) 设函数![]() ,求函数h(x)的极值;
,求函数h(x)的极值;
(Ⅲ) 若![]() 在[1,e](e=2.718 28…)上存在一点x0,使得
在[1,e](e=2.718 28…)上存在一点x0,使得![]() 成立,求a的取值范围.
成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 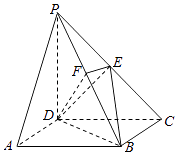
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列命题:
①乘积(a+b+c+d)(p+q+r)(m+n)展开式的项数是24;
②由1、2、3、4、5组成没有重复数字且1、2都不与5相邻的五位数的个数是36;
③某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为24;
④已知(1+x)8=a0+a1x+…+a8x8 , 其中a0 , a1 , …,a8中奇数的个数为2.
其中真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C焦点在y轴上,离心率为 ![]() ,上焦点到上顶点距离为2﹣
,上焦点到上顶点距离为2﹣ ![]() .
.
(1)求椭圆C的标准方程;
(2)直线l与椭圆C交与P,Q两点,O为坐标原点,△OPQ的面积S△OPQ=1,则| ![]() |2+|
|2+| ![]() |2是否为定值,若是求出定值;若不是,说明理由.
|2是否为定值,若是求出定值;若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com