
A.0<a≤1
B.a<1
C.a≤1
D.0<a≤1或a<0
错解:方程ax2+2x+1=0有实根的充要条件是判别式Δ≥0,即4
(1)又设方程ax2+2x+1=0的根为x1、x2,由韦达定理知x1+x2=-![]() ,x1·x2=
,x1·x2=![]() ,
,
因而方程ax2+2x+1=0有1个负根的充要条件是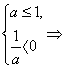 a<0.
a<0.
(2)方程ax2+2x+1=0有2个负根的充要条件是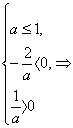 0<a≤1.
0<a≤1.
综上所述,本题应选D.
错解分析:由于方程的二次项系数含有字母,因此,首先要判定方程ax2+2x+1=0是一元一次方程还是一元二次方程.求充要条件时,要保证推理过程可逆.
正解:(1)当a=0时,方程就是2x+1=0,其根为x=-![]() ,符合要求;
,符合要求;
(2)当a≠0时,它为一元二次方程,又要分方程有一个负根一个正根,两个都是负根.解法见错解,得a<0或0<a≤1.(没有零根)
由(1)(2)知,本题选C.
答案:C


科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com