
| ���� | ||||
| �� | �� | ���� | ||
| ��ѧ | �� | 8 | m | 9 |
| �� | 9 | n | 11 | |
| ���� | 8 | 9 | 11 | |
���� ������$\frac{8+m+9}{100}$=0.35�����m���ɴ������n��
����������m+n=35����m��12��n��10�������оٷ�������������ģ�m��n���Ļ����¼��������ǣ�����ѧ�ɼ���������������������١�Ϊ�¼�M�������оٷ�����¼�M�����Ļ����¼��������ɴ�����������
��� �⣺������$\frac{8+m+9}{100}$=0.35����m=18
��Ϊ8+9+8+18+n+9+9+11+11=100��
����n=17��
����������m+n=35����m��12��n��10��
�������������ģ�m��n���У�
��12��23������13��22������14��21������15��20������16��19������17��18������18��17����
��19��16������20��15������21��14������22��13������23��12������24��11������25��10����
����14�֣���ÿ����ֶ��ǵȿ��ܵģ�
�ǣ�����ѧ�ɼ���������������������١�Ϊ�¼�M��
�¼�M��������12��23������13��22������14��21������15��20������16��19������17��18����6�������¼���
��P��M��=$\frac{6}{14}=\frac{3}{7}$������12�֣�
���� ���⿼����ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
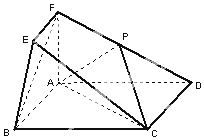 ����ͼ��ʾ�ļ������У��ı���ABCDΪ���Σ�ƽ��ABEF��ƽ��ABCD��EF��AB����BAF=90�㣬AD=2��AB=AF=2EF=l����P����DF�ϣ�
����ͼ��ʾ�ļ������У��ı���ABCDΪ���Σ�ƽ��ABEF��ƽ��ABCD��EF��AB����BAF=90�㣬AD=2��AB=AF=2EF=l����P����DF�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ∅ | B�� | {1} | C�� | {0��1��2} | D�� | {2��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com