
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若函数f(x)=lnx与函数g(x)=x2+2x+lna(x<0)有公切线,则实数a的取值范围是( )
A.(0,1)B.![]() C.(1,+∞)D.
C.(1,+∞)D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点的距离为
到焦点的距离为![]() ,过
,过![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() 和
和![]() ,其中斜率为
,其中斜率为![]()
![]() 与抛物线交于A,B,
与抛物线交于A,B,![]() 与y轴交于C,点Q满足:
与y轴交于C,点Q满足:![]()
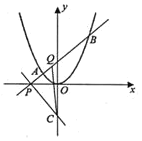
(1)求抛物线的方程;
(2)求三角形PQC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为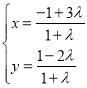 (
(![]() 为参数,且
为参数,且![]() ).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线
).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点P的极坐标为![]() ,Q为曲线
,Q为曲线![]() 上的动点,求
上的动点,求![]() 的中点M到曲线
的中点M到曲线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)证明:当![]() 时,
时,![]() 在
在![]() 上有两个极值点;
上有两个极值点;
(3)设![]() ,若
,若![]() 在
在![]() 上是单调减函数(
上是单调减函数(![]() 为自然对数的底数),求实数
为自然对数的底数),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司年会有幸运抽奖环节,一个箱子里有相同的十个兵乓球,球上分别标0,1,2,…,9这十个自然数,每位员工有放回的依次取出三个球.规定:每次取出的球所标数字不小于后面取出的球所标数字即中奖.中奖奖项:三个数字全部相同中一等奖,奖励10000元现金;三个数字中有两个数字相同中二等奖,奖励5000元现金;三个数字各不相同中三等奖,奖励2000元现金;其它不中奖,没有奖金.
(1)求员工A中二等奖的概率;
(2)设员工A中奖奖金为X,求X的分布列;
(3)员工B是优秀员工,有两次抽奖机会,求员工B中奖奖金的期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com