
【题目】2018年2月22日.在平昌冬奥会短道速滑男子500米比赛中.中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况.收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人.已知这20位女生的数据茎叶图如图所示.
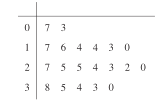
(1)将这20位女生的时间数据分成8组,分组区间分别为![]() ,在答题卡上完成频率分布直方图;
,在答题卡上完成频率分布直方图;
(2)以(1)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;
(3)以(1)中的频率估计100位女生中累计观看时间小于20个小时的人数.已知200位男生中累计观看时间小于20小时的男生有50人请完成答题卡中的列联表,并判断是否有99 %的把握认为“该校学生观看冬奥会累计时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
【答案】(1)见解析(2)![]() (3)有99%的把握
(3)有99%的把握
【解析】分析:(1)由题意知样本容量为![]() ,得到频率分布表,进而得到频率分布直方图.
,得到频率分布表,进而得到频率分布直方图.
(2)因为(1)中![]() 的频率为
的频率为![]() ,进而得到
,进而得到![]() 名女生观看冬奥会时间不少于
名女生观看冬奥会时间不少于![]() 小时的概率;
小时的概率;
(3)因为(1),根据题意,得出![]() 列联表,求得
列联表,求得![]() 的值,即可作出判断.
的值,即可作出判断.
详解:解:(1)由题意知样本容量为![]() ,频率分布表如下:
,频率分布表如下:
分组 | 频数 | 频率 |
|
| 1 |
| 0.01 |
| 1 |
| 0.01 |
| 4 |
| 0.04 |
| 2 |
| 0.02 |
| 4 |
| 0.04 |
| 3 |
| 0.03 |
| 3 |
| 0.03 |
| 2 |
| 0.02 |
合计 | 20 | 1 |
频率分布直方图为:

(2)因为(1)中![]() 的频率为
的频率为![]() ,
,
所以![]() 名女生观看冬奥会时间不少于
名女生观看冬奥会时间不少于![]() 小时的概率为
小时的概率为![]() .
.
(3)因为(1)中![]() 的频率为
的频率为![]() ,故可估计
,故可估计![]() 位女生中累计观看时间小于
位女生中累计观看时间小于![]() 小时的人数是
小时的人数是![]() .所以累计观看时间与性别列联表如下:
.所以累计观看时间与性别列联表如下:
男生 | 女生 | 总计 | |
累计观看时间小于20小时 | 50 | 40 | 90 |
累计观看时间不小于20小时 | 150 | 60 | 210 |
总计 | 200 | 100 | 300 |
结合列联表可算得
![]() ,
,
所以,有![]() 的把握认为“该校学生观看冬奥会累计时间与性别有关”.
的把握认为“该校学生观看冬奥会累计时间与性别有关”.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】将一个总体的100个个体编号为0,1,2,…,99,并依次将其分为10个组,组号为0,1,2,…,9.要用系统抽样法抽取一个容量为10的样本,如果在第0组(号码为0—9)随机抽取的号码为2,则抽取的10个号码为______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中心在原点,焦点在![]() 轴上的椭圆,下顶点
轴上的椭圆,下顶点![]() ,且离心率
,且离心率![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两点.在
两点.在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点
恒成立?若存在,求出点![]() 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,直线
,直线![]() 过点
过点![]() 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线![]() 垂直
垂直![]() 于点
于点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)当直线![]() 与椭圆
与椭圆![]() 相切,交
相切,交![]() 于点
于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假定小麦基本苗数![]() 与成熟期有效穗
与成熟期有效穗![]() 之间存在相关关系,今测得5组数据如下:
之间存在相关关系,今测得5组数据如下:

(1)以![]() 为解释变量,
为解释变量,![]() 为预报变量,画出散点图
为预报变量,画出散点图
(2)求![]() 与
与![]() 之间的回归方程
之间的回归方程
(3)当基本苗数为![]() 时预报有效穗(注:
时预报有效穗(注: ,
, ![]() )
)![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数不超过20人,每人需交费用800元;若旅行团人数超过20人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数60人为止.旅行社需支付各种费用共计10000元.
(1)写出每人需交费用S关于旅行团人数![]() 的函数;
的函数;
(2)旅行团人数x为多少时,旅行社可获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com