
【题目】在平面直角坐标系中,点![]() 是直线
是直线![]() 上的动点,定点
上的动点,定点![]() 点
点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 两点,
两点,![]() 为
为![]() 上任意一点,直线
上任意一点,直线![]() 交
交![]() 于
于![]() 两点,以
两点,以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
轴上的定点? 若过定点,求出定点的坐标;若不过定点,说明理由。
【答案】(1)![]() (2)以
(2)以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]()
【解析】分析:(1)根据条件可得点![]() 的轨迹是以
的轨迹是以![]() 为焦点、以直线
为焦点、以直线![]() 为准线的抛物线,其方程为
为准线的抛物线,其方程为![]() .(2)假设以
.(2)假设以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]() , 设
, 设![]()
![]()
![]() .由题意可得
.由题意可得![]() ,
,![]() ,由
,由![]() 得
得![]() .设直线
.设直线![]() 的方程为
的方程为![]() ,与抛物线方程联立消元后得到二次方程,结合根与系数的关系和上式可得
,与抛物线方程联立消元后得到二次方程,结合根与系数的关系和上式可得![]() ,解得
,解得![]() ,进而可得以
,进而可得以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]() .
.
详解:(1)由已知得![]() 垂直平分
垂直平分![]() ,故
,故![]()
又![]() 轴,
轴,
则![]() ,
,
所以点![]() 到点
到点![]() 的距离和到直线
的距离和到直线![]() 的距离相等,
的距离相等,
故点![]() 的轨迹是以
的轨迹是以![]() 为焦点、以直线
为焦点、以直线![]() 为准线的抛物线,
为准线的抛物线,
由条件可得轨迹的方程为![]() .
.
(2)假设以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]() .
.
设![]()
![]()
![]() ,
,
则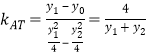 ,
,
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() 即
即![]() .
.
同理可得![]() .
.
由已知得![]() 恒成立,即
恒成立,即![]() ,
,
即![]() .
.
设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去
消去![]() 整理得
整理得![]() ,
,
所以![]() ,
,
于是![]() ,
,
整理得![]() ,
,
解得![]() .
.
故以![]() 为直径的圆过
为直径的圆过![]() 轴上的定点
轴上的定点![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<![]() )的图象与x轴的交点中,相邻两条对称轴之间的距离为
)的图象与x轴的交点中,相邻两条对称轴之间的距离为![]() ,且图象上一个最低点为M
,且图象上一个最低点为M![]() .
.
(1)求ω,φ的值;
(2)求f(x)的图像的对称中心;
(3)当x∈![]() 时,求f(x)的值域.
时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是线段BC,AB的中点.
,E,F是线段BC,AB的中点.

![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在线段PA上确定点G,使得
在线段PA上确定点G,使得![]() 平面PED,请说明理由.
平面PED,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B、C三位老师分别教数学、英语、体育、劳技、语文、阅读六门课,每位教两门.已知:
(1)体育老师和数学老师住在一起,
(2)A老师是三位老师中最年轻的,
(3)数学老师经常与C老师下象棋,
(4)英语老师比劳技老师年长,比B老师年轻,
(5)三位老师中最年长的老师比其他两位老师家离学校远.
问:A、B、C三位老师每人各教哪几门课?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体![]() 中,
中, ![]() 在平面
在平面![]() 的射影
的射影![]() 为棱
为棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 的中点,过直线
的中点,过直线![]() 作一个平面与平面
作一个平面与平面![]() 平行,且与
平行,且与![]() 交于点
交于点![]() ,已知
,已知![]() ,
, ![]() .
.

(1)证明: ![]() 为线段
为线段![]() 的中点
的中点
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的一元二次方程![]() 有两个不相等的实数根;命题q:关于x的一元二次方程
有两个不相等的实数根;命题q:关于x的一元二次方程![]() 对于任意实数a都没有实数根.
对于任意实数a都没有实数根.
![]() 若命题p为真命题,求实数m的取值范围;
若命题p为真命题,求实数m的取值范围;
![]() 若命题p和命题q中有且只有一个为真命题,求实数m的取值范围.
若命题p和命题q中有且只有一个为真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC= ![]() AB,若四面体P﹣ABC的体积为
AB,若四面体P﹣ABC的体积为 ![]() ,则该球的体积为( )
,则该球的体积为( )
A.![]()
B.2π
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示. 
(1)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由;(下面的临界值表供参考) (参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)现计划在这次场外调查中按年龄段选取6名选手,并抽取3名幸运选手,求3名幸运选手中在20~30岁之间的人数的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com