
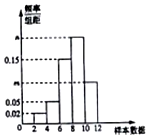
 有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )
有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )| A. | 0.10 | B. | 0.11 | C. | 0.12 | D. | 0.13 |
分析 根据题意,求出样本数据落在区间[10,12)和[8,10)内的频率、频数和,再求出样本数据落在区间[8,10)内的频率,利用$\frac{频率}{组距}$求出m的值.
解答 解:根据题意,样本数据落在区间[10,12)和[8,10)内的频率和为:
1-(0.02+0.05+0.15)×2=0.56,
所以频数和为100×0.56=56,
又样本数据落在区间[10,12)内的频数比落在区间[8,10)内的频数少12,
所以样本数据落在区间[8,10)内的频率为$\frac{0.56-0.12}{2}$=0.22,
所以m=$\frac{0.22}{2}$=0.11.
故选:B.
点评 本题考查了频数,频率及频率分布直方图,运用统计知识解决实际问题、数据处理能力,是基础题目.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
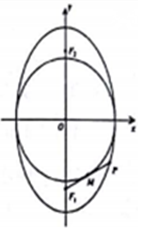 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
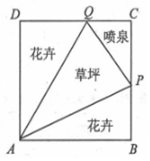 如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.
如图所示,我市某居民小区拟在边长为1百米的正方形地块ABCD上划出一个三角形地块APQ种植草坪,两个三角形地块PAB与QAD种植花卉,一个三角形地块CPQ设计成水景喷泉,四周铺设小路供居民平时休闲散步,点P在边BC上,点Q在边CD上,记∠PAB=a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com