
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
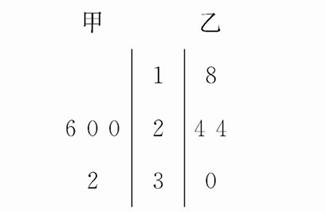
(1)求乙球员得分的平均数和方差;
(2)分别从两人得分中随机选取一场的得分,求得分和Y的分布列和数学期望.
(注:方差s2=![]() [(x1-
[(x1-![]() )2+(x2-
)2+(x2-![]() )2+…+(xn-
)2+…+(xn-![]() )2],其中
)2],其中![]() 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
(1)由茎叶图可知,乙球员四场比赛得分为18,24,24,30,所以平均数为
![]() =
=![]() =24;
=24;
方差为:s2=![]() [(18-24)2+(24-24)2+(24-24)2+(30-24)2]=18.
[(18-24)2+(24-24)2+(24-24)2+(30-24)2]=18.
(2)甲球员四场比赛得分为20,20,26,32,分别从两人得分中随机选取一场的得分,共有16种情况:
(18,20)(18,20)(18,26)(18,32)
(24,20)(24,20)(24,26)(24,32)
(24,20)(24,20)(24,26)(24,32)
(30,20)(30,20)(30,26)(30,32)
得分和可能的结果有:38,44,50,56,62
得分和Y的分布列为:
| Y | 38 | 44 | 50 | 56 | 62 |
| P |
|
|
|
|
|
数学期望E(Y)=38×![]() +44×
+44×![]() +50×
+50×![]() +56×
+56×![]() +62×
+62×![]() =48.5.
=48.5.


科目:高中数学 来源: 题型:
 甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
 2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是
2012年的NBA全明星赛,于美国当地时间2012年2月26日在佛罗里达州奧兰多市举行.如图是参加此次比赛的甲、乙两名篮球运动员以往几场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是查看答案和解析>>
科目:高中数学 来源: 题型:
 某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下(单位:分):
. | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com