
【题目】给定数列![]() .对
.对![]() ,该数列前
,该数列前![]() 项
项![]() 的最小值记为
的最小值记为![]() ,后
,后![]() 项
项![]() 的最大值记为
的最大值记为![]() ,令
,令![]() .
.
(1)设数列![]() 为2,1,6,3,写出
为2,1,6,3,写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)设![]() 是等比数列,公比
是等比数列,公比![]() ,且
,且![]() ,证明:
,证明:![]() 是等比数列;
是等比数列;
(3)设![]() 是公差大于0的等差数列,且
是公差大于0的等差数列,且![]() ,证明:
,证明:![]() 是等差数列.
是等差数列.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)证明见解析;(3)证明见解析
;(2)证明见解析;(3)证明见解析
【解析】
(1)求出![]() 及
及![]() 的值,并结合
的值,并结合![]() ,可求出
,可求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)易知数列![]() 是递减数列,从而可知
是递减数列,从而可知![]() 时,
时,![]() ,
,![]() ,可得
,可得![]() ,且
,且![]() ,进而可得
,进而可得![]() ,从而可知
,从而可知![]() 为定值,即可证明结论成立;
为定值,即可证明结论成立;
(3)![]() 是等差数列,先用反证法证明
是等差数列,先用反证法证明![]() 是单调递减数列,再用反证法证明
是单调递减数列,再用反证法证明![]() 为数列
为数列![]() 中的最大项,从而可知
中的最大项,从而可知![]()
![]() ,则
,则![]() ,进而可证明结论成立.
,进而可证明结论成立.
(1)由题意,![]() ,则
,则![]() ;
;
![]() ,则
,则![]() ;
;
![]() ,则
,则![]() .
.
(2)因为![]() 是等比数列,公比
是等比数列,公比![]() ,且
,且![]() ,所以数列
,所以数列![]() 是递减数列,
是递减数列,
则![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以![]() 时,
时,![]() ,
,
所以![]() ,即
,即![]() 是等比数列.
是等比数列.
(3)由![]() 是公差大于0的等差数列,且
是公差大于0的等差数列,且![]() ,可知
,可知![]() .
.
①先用反证法证明![]() 是递减数列,
是递减数列,
假设![]() 不是递减数列,设
不是递减数列,设![]() 是第一个使得
是第一个使得![]() 成立的项,则
成立的项,则![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,与
,与![]() 相矛盾,
相矛盾,
所以![]() 是单调递减数列.
是单调递减数列.
②再用反证法证明![]() 为数列
为数列![]() 中的最大项,
中的最大项,
假设![]() 不是数列
不是数列![]() 的最大项,即存在
的最大项,即存在![]()
![]() 使得
使得![]() 成立,
成立,
若![]() 时,满足
时,满足![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,与
,与![]() 矛盾,即
矛盾,即![]() ;
;
若![]() 时,满足
时,满足![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,与
,与![]() 矛盾,
矛盾,
所以![]() 为数列
为数列![]() 中的最大项.
中的最大项.
综上,![]() 是单调递减数列,且
是单调递减数列,且![]() 为数列
为数列![]() 中的最大项,
中的最大项,
故![]()
![]() ,即
,即![]() ,
,
则![]() 时,
时,![]() ,
,
故![]()
![]() ,
,
所以![]() 是等差数列.
是等差数列.


科目:高中数学 来源: 题型:
【题目】已知直线![]() 与函数
与函数![]() (
(![]() )的图象相交,将其中三个相邻交点从左到右依次记为A,B,C,且满足
)的图象相交,将其中三个相邻交点从左到右依次记为A,B,C,且满足![]()
![]() 有下列结论:
有下列结论:
①n的值可能为2
②当![]() ,且
,且![]() 时,
时,![]() 的图象可能关于直线
的图象可能关于直线![]() 对称
对称
③当![]() 时,有且仅有一个实数ω,使得
时,有且仅有一个实数ω,使得![]() 在
在![]() 上单调递增;
上单调递增;
④不等式![]() 恒成立
恒成立
其中所有正确结论的编号为( )
A.③B.①②C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,角
中,角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,________.是否存在以
,________.是否存在以![]() ,
,![]() ,
,![]() 为边的三角形?如果存在,求出
为边的三角形?如果存在,求出![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
从①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选一个,补充在上面问题中并作答.
这三个条件中任选一个,补充在上面问题中并作答.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
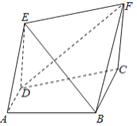
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有一题:今有牛、马、羊食人苗,苗主责之粟四斗.羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?其意是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿4斗粟,羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比率偿还,牛、马、羊的主人各应赔偿多少粟?在这个问题中,牛主人比羊主人多赔偿了多少斗( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )

A.28B.56C.84D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com