
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD‖BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD‖BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=$\sqrt{3}$.分析 (Ⅰ)法一:由AD∥BC,BC=$\frac{1}{2}$AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知QB⊥AD.由平面PAD⊥平面ABCD,知BQ⊥平面PAD.由此能够证明平面PQB⊥平面PAD.
法二:由AD∥BC,BC=$\frac{1}{2}$AD,Q为AD的中点,知四边形BCDQ为平行四边形,故CD∥BQ.由∠ADC=90°,知∠AQB=90°.由PA=PD,知PQ⊥AD,故AD⊥平面PBQ.由此证明平面PQB⊥平面PAD.
(Ⅱ)由PA=PD,Q为AD的中点,知PQ⊥AD.由平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,知PQ⊥平面ABCD.以Q为原点建立空间直角坐标系,利用向量法能够求出t=3.
解答  证明:(Ⅰ)证法一:∵AD∥BC,BC=1,AD=2,Q为AD的中点,
证明:(Ⅰ)证法一:∵AD∥BC,BC=1,AD=2,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD∥BQ.
∵∠ADC=90°
∴∠AQB=90°,即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(9分)
证法二:AD∥BC,BC=1,AD=2,Q为AD的中点,
∴四边形BCDQ为平行四边形,
∴CD∥BQ.
∵∠ADC=90°
∴∠AQB=90°.
∵PA=PD,
∴PQ⊥AD.
∵PQ∩BQ=Q,
∴AD⊥平面PBQ.
∵AD?平面PAD,
∴平面PQB⊥平面PAD.…(9分)
(Ⅱ)∵PA=PD,Q为AD的中点,
∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为$\overrightarrow n=(0,0,1)$;
Q(0,0,0),$P(0,0,\sqrt{3})$,$B(0,\sqrt{3},0)$,$C(-1,\sqrt{3},0)$.
设M(x,y,z),则$\overrightarrow{PM}=(x,y,z-\sqrt{3})$,$\overrightarrow{MC}=(-1-x,\sqrt{3}-y,-z)$,
∵$\overrightarrow{PM}=t\overrightarrow{MC}$,
∴$\left\{\begin{array}{l}x=t(-1-x)\\ y=t(\sqrt{3}-y)\\ z-\sqrt{3}=t(-z)\end{array}\right.$,∴$\left\{\begin{array}{l}x=-\frac{t}{1+t}\\ y=\frac{{\sqrt{3}t}}{1+t}\\ z=\frac{{\sqrt{3}}}{1+t}\end{array}\right.$…(12分)
在平面MBQ中,$\overrightarrow{QB}=(0,\sqrt{3},0)$,$\overrightarrow{QM}=(-\frac{t}{1+t},\frac{{\sqrt{3}t}}{1+t},\frac{{\sqrt{3}}}{1+t})$,
∴平面MBQ法向量为$\overrightarrow m=(\sqrt{3},0,t)$.…(13分)
∵二面角M-BQ-C为30°,
∴$cos{30°}=\frac{\overrightarrow n•\overrightarrow m}{{|{\overrightarrow n}||{\overrightarrow m}|}}=\frac{t}{{\sqrt{3+0+{t^2}}}}=\frac{{\sqrt{3}}}{2}$,
∴t=3.…(15分)
点评 本题主要考查空间面面垂直的判断以及二面角的求解,建立坐标系,求出平面的法向量,利用向量法是解决本题的关键.解题时要认真审题,仔细解答,注意合理地进行等价转化,合理地运用向量法进行解题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -2 | C. | 2 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
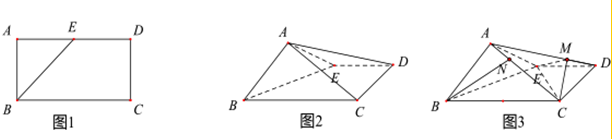
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
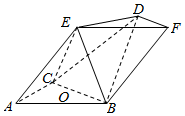 如图,多面体ABCDEF中,四边形ABEF是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.
如图,多面体ABCDEF中,四边形ABEF是平行四边形,DF∥BC,BC=BF=2DF=2$\sqrt{2}$,∠BAC=90°,AB=AC,点E在底面ABC的射影为BC的中点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com