
【题目】流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:
年龄( |
|
|
|
|
|
患病人数( |
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)计算变量![]() 、
、![]() 的相关系数
的相关系数![]() (计算结果精确到
(计算结果精确到![]() ),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若
),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若![]() ,则
,则![]() 、
、![]() 相关性很强;若
相关性很强;若![]() ,则
,则![]() 、
、![]() 相关性一般;若
相关性一般;若![]() ,则
,则![]() 、
、![]() 相关性较弱.)
相关性较弱.)
参考数据:![]() .
.
参考公式: ,
,
相关系数 .
.
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 既有一个极小值又有一个极大值,求
既有一个极小值又有一个极大值,求![]() 的取值范围;
的取值范围;
(3)若存在![]() ,使得当
,使得当![]() 时,
时, ![]() 的值域是
的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
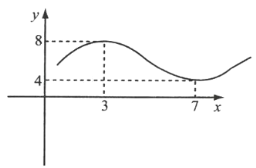
【题目】据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈![]() 的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为
的模型波动(x为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为![]() (x为月份),且满足
(x为月份),且满足![]() .
.
(1)分别写出该商品每件的出厂价函数![]() 和售价函数
和售价函数![]() 的解析式;
的解析式;
(2)问几月份的销售盈利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为打赢脱贫攻坚战,解决脱贫问题,政府重点扶持扶贫工厂.当地对某扶贫工厂进行设备改造,为分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取100件产品作为样本,检测质量指标值![]() .该产品为次品、合格品、优等品所对应的指标值范围分别为
.该产品为次品、合格品、优等品所对应的指标值范围分别为![]() ,
,![]() ,
,![]() .设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
.设备改造前的样本的频率分布直方图如图所示,设备改造后的样本的频数分布表如下所示.
质量指标值 |
|
|
|
|
|
频数 | 1 | 4 | 47 | 38 | 10 |

(Ⅰ)根据以上数据,完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为设备改造与产品为次品有关?
的把握认为设备改造与产品为次品有关?
次品 | 非次品 | 合计 | |
改造前 | |||
改造后 | |||
合计 |
(Ⅱ)若工人的月工资是由基本工资1000元与效益工资两部分组成.效益工资实施细则如下:每生产一件产品是合格品的奖50元,是优等品的奖100元,是次品的扣20元.将频率视为概率,估计设备改造后,一个月生产60件产品的工人月工资为多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,以
,以![]() 为圆心的圆记为圆
为圆心的圆记为圆![]() ,已知圆
,已知圆![]() 上的点与圆
上的点与圆![]() 上的点之间距离的最大值为21.
上的点之间距离的最大值为21.
(1)求圆![]() 的标准方程;
的标准方程;
(2)求过点![]() 且与圆
且与圆![]() 相切的直线的方程;
相切的直线的方程;
(3)已知直线![]() 与
与![]() 轴不垂直,且与圆
轴不垂直,且与圆![]() ,圆
,圆![]() 都相交,记直线
都相交,记直线![]() 被圆
被圆![]() ,圆
,圆![]() 截得的弦长分别为
截得的弦长分别为![]() ,
,![]() .若
.若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始________h后,两车的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第
,则第![]() 次改良后所排放的废气中的污染物数量
次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中
给出,其中![]() 是指改良工艺的次数.
是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com