
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
【答案】(Ⅰ) ![]() ;
;
(Ⅱ)见解析;
(Ⅲ)见解析.
【解析】
(Ⅰ)由题意利用古典概型计算公式可得满足题意的概率值;
(Ⅱ)首先确定X可能的取值,然后求得相应的概率值可得分布列,最后求解数学期望即可.
(Ⅲ)由题意结合概率的定义给出结论即可.
(Ⅰ)由题意可知,两种支付方式都是用的人数为:![]() 人,则:
人,则:
该学生上个月A,B两种支付方式都使用的概率![]() .
.
(Ⅱ)由题意可知,
仅使用A支付方法的学生中,金额不大于1000的人数占![]() ,金额大于1000的人数占
,金额大于1000的人数占![]() ,
,
仅使用B支付方法的学生中,金额不大于1000的人数占![]() ,金额大于1000的人数占
,金额大于1000的人数占![]() ,
,
且X可能的取值为0,1,2.
![]() ,
,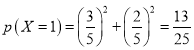 ,
,![]() ,
,
X的分布列为:
X | 0 | 1 | 2 |
|
|
|
|
其数学期望:![]() .
.
(Ⅲ)我们不认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化.理由如下:
随机事件在一次随机实验中是否发生是随机的,是不能预知的,随着试验次数的增多,频率越来越稳定于概率。
学校是一个相对消费稳定的地方,每个学生根据自己的实际情况每个月的消费应该相对固定,出现题中这种现象可能是发生了“小概率事件”.


科目:高中数学 来源: 题型:
【题目】已知![]() 表示两个不同的平面,
表示两个不同的平面, ![]() 表示两条不同直线,对于下列两个命题:
表示两条不同直线,对于下列两个命题:
①若![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②若![]() ,则“
,则“![]() ”是“
”是“![]() 且
且![]() ”的充要条件.判读正确的是( )
”的充要条件.判读正确的是( )
A. ①②都是真命题 B. ①是真命题,②是假命题
C. ①是假命题,②是真命题 D. ①②都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校计划举办“国学”系列讲座.由于条件限制,按男、女生比例采取分层抽样的方法,从某班选出10人参加活动,在活动前,对所选的10名同学进行了国学素养测试,这10名同学的性别和测试成绩(百分制)的茎叶图如图所示.

(1)分别计算这10名同学中,男女生测试的平均成绩;
(2)若这10名同学中,男生和女生的国学素养测试成绩的标准差分别为S1,S2,试比较S1与S2的大小(不必计算,只需直接写出结果);
(3)规定成绩大于等于75分为优良,从这10名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优良的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )与双曲线
)与双曲线![]() (
(![]() ,
,![]() )有相同的焦点
)有相同的焦点![]() ,点
,点![]() 是两条曲线的一个交点,且
是两条曲线的一个交点,且![]() 轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
轴,则该双曲线经过一、三象限的渐近线的倾斜角所在的区间是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:存在正整数
满足:存在正整数![]() ,对任意的
,对任意的![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为
为![]() 阶稳增数列.
阶稳增数列.
(1)若由正整数构成的数列![]() 为
为![]() 阶稳增数列,且对任意
阶稳增数列,且对任意![]() ,数列
,数列![]() 中恰有
中恰有![]() 个
个![]() ,求
,求![]() 的值;
的值;
(2)设等比数列![]() 为
为![]() 阶稳增数列且首项大于
阶稳增数列且首项大于![]() ,试求该数列公比
,试求该数列公比![]() 的取值范围;
的取值范围;
(3)在(1)的条件下,令数列![]() (其中
(其中![]() ,常数
,常数![]() 为正实数),设
为正实数),设![]() 为数列
为数列![]() 的前
的前![]() 项和.若已知数列
项和.若已知数列![]() 极限存在,试求实数
极限存在,试求实数![]() 的取值范围,并求出该极限值.
的取值范围,并求出该极限值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:

①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个;
,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(Ⅰ)求小亮获得玩具的概率;
(Ⅱ)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2ax2+2bx,若存在实数x0∈(0,t),使得对任意不为零的实数a,b均有f(x0)=a+b成立,则t的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
(1)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的斜率;
的斜率;
(2)在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,极坐标方程为
轴正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com