
【题目】(1)已知数列![]() 的通项公式:
的通项公式:![]() ,试求
,试求![]() 最大项的值;
最大项的值;
(2)记![]() ,且满足(1),若
,且满足(1),若![]() 成等比数列,求p的值;
成等比数列,求p的值;
(3)如果![]() ,
,![]() ,
,![]() ,且p是满足(2)的正常数,试证:对于任意自然数n,或者都满足
,且p是满足(2)的正常数,试证:对于任意自然数n,或者都满足![]() ,
,![]() ,或者都满足
,或者都满足![]() ,
,![]() .
.
 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】某校高一年级模仿《中国诗词大会》节目举办学校诗词大会,进入正赛的条件为:电脑随机抽取10首古诗,参赛者能够正确背诵6首及以上的进入正赛,若学生甲参赛,他背诵每一首古诗的正确的概率均为![]()
(1)求甲进入正赛的概率;
(2)若进入正赛,则采用积分淘汰制,规则是:电脑随机抽取4首古诗,每首古诗背诵正确加2分,错误减1分.由于难度增加,甲背诵每首古诗正确的概率为![]() ,求甲在正赛中积分
,求甲在正赛中积分![]() 的概率分布列及数学期望.
的概率分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,点
是菱形,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是线段
是线段![]() 的中点,且三棱锥
的中点,且三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() .
.
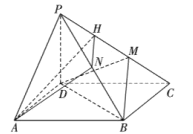
(1)若![]() 是
是![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A-BCD中,AD⊥BD,AC⊥BC,∠DAB=![]() ,∠BAC=
,∠BAC=![]() .三棱锥的外接球的表面积为16π,则该三棱锥的体积的最大值为( )
.三棱锥的外接球的表面积为16π,则该三棱锥的体积的最大值为( )
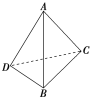
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某小区2017年1月至2018年1月当月在售二手房均价(单位:万元/平方米)的散点图.(图中月份代码1—13分别对应2017年1月—2018年1月)
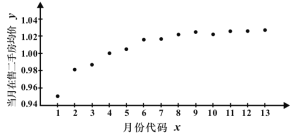
由散点图选择![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程分别为
两个模型进行拟合,经过数据处理得到两个回归方程分别为![]() 和
和![]() ,并得到以下一些统计量的值:
,并得到以下一些统计量的值:
|
| |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数![]() 判断哪个模型的拟合效果更好;
判断哪个模型的拟合效果更好;
(2)某位购房者拟于2018年6月份购买这个小区![]() 平方米的二手房(欲
平方米的二手房(欲
购房为其家庭首套房).若购房时该小区所有住房的房产证均已满2年但未满5年,请你利用(1)中拟合效果更好的模型估算该购房者应支付的购房金额.(购房金额=房款+税费;房屋均价精确到0.001万元/平方米)
附注:根据有关规定,二手房交易需要缴纳若干项税费,税费是按房屋的计税价格进行征收.(计税价格=房款),征收方式见下表:
契税 (买方缴纳) | 首套面积90平方米以内(含90平方米)为1%;首套面积90平方米以上且144平方米以内(含144平方米)为1.5%;面积144平方米以上或非首套为3% |
增值税 (卖方缴纳) | 房产证未满2年或满2年且面积在144平方米以上(不含144平方米)为5.6%;其他情况免征 |
个人所得税 (卖方缴纳) | 首套面积144平方米以内(含144平方米)为1%;面积144平方米以上或非首套均为1.5%;房产证满5年且是家庭唯一住房的免征 |
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() . 参考公式:相关指数
. 参考公式:相关指数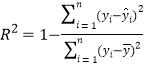 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有两个国家AAAA级景区—甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的客流量(单位:百人),得到如图所示的茎叶图.关于2019年1月至6月这两个景区的客流量,下列结论正确的是( )
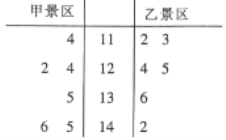
A.甲景区客流量的中位数为13000
B.乙景区客流量的中位数为13000
C.甲景区客流量的平均值比乙景区客流量的平均值小
D.甲景区客流量的极差比乙景区客流量的极差大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 是抛物线上关于
是抛物线上关于![]() 轴对称的两点,点
轴对称的两点,点![]() 是抛物线准线
是抛物线准线![]() 与
与![]() 轴的交点,
轴的交点,![]() 是面积为
是面积为![]() 的直角三角形.
的直角三角形.
(1)求抛物线的方程;
(2)点![]() 在抛物线上,
在抛物线上,![]() 是直线
是直线![]() 上不同的两点,且线段
上不同的两点,且线段![]() 的中点都在抛物线上,试用
的中点都在抛物线上,试用![]() 表示
表示![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com