已知函数f(x)=x3+bx2+cx+d在(-∞,0)上为增函数,在[0,2]上为减函数,又方程f(x)=0有三个根α,2,β.
(I)求c的值并比较f(l)与2的大小;
(II)求|α-β|的取值范围.
解:(I)∵f′(x)=3x
2+2bx+c
∵函数f(x)=x
3+bx
2+cx+d在(-∞,0)上为增函数,在[0,2]上为减函数
∴函数f(x)在x=0时取得极值,即f′(0)=0
∴c=0
∴f(1)=1+b+d
又f′(x)=3x
2+2bx的两根为0,-
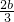
,而方程f(x)=0有三个根α,2,β.
∴-
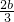
≥2,且8+4b+d=0
∴b≤-3且d=-8-4b
∴f(1)=1+b-8-4b=-7-3b≥2
(Ⅱ)∵f(x)=(x-α)(x-2)(x-β)=x
3-(α+β+2)•x
2-2αβ
∴α+β+2=-b,-2αβ=d;
∴|β-α|
2=(α+β)
2-4αβ
=(b+2)
2+2d
=b
2+4b+4-16-8b
=b
2-4b-12
=(b-2)
2-16
又∵b≤-3,
∴|β-α|
2≥25-16=9
∴|β-α|≥3
当且仅当b=-3时取最小值,此时d=4
故|α-β|的取值范围为[3,+∞)
分析:(I)利用已知函数的单调性可判断函数的一个极值点为x=0,由f′(0)=0即可得c的值,再利用函数的极值点应该在函数的零点之间,且方程的一个零点为2的特点,比较f(l)与2的大小
(II)由于方程f(x)=0有三个根α,2,β.故可设函数为f(x)=(x-α)(x-2)(x-β),展开后找到α、β与b、d的关系,进而利用(I)中的结论,将|α-β|的平方表示为关于b的一元函数,求其取值范围即可
点评:本题主要考查了导数在函数极值中的应用,三次函数的根与极值点间的关系,将变量表示为关于另一变量的函数的能力,代数变换能力,转化化归的思想方法

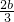 ,而方程f(x)=0有三个根α,2,β.
,而方程f(x)=0有三个根α,2,β.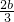 ≥2,且8+4b+d=0
≥2,且8+4b+d=0

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<