
ΓΨΧβΡΩΓΩΈΣΝΥΝΥΫβΡ≥≥« –Ψ”Οώ”ΟΥ°ΝΩΒΡ«ιΩωΘ§Έ“Ο«ΜώΒΟ100ΈΜΨ”ΟώΡ≥ΡξΒΡ‘¬Ψυ”ΟΥ°ΝΩΘ®ΒΞΈΜΘΚΕ÷Θ©Ά®ΙΐΕ‘ ΐΨίΒΡ¥ΠάμΘ§Έ“Ο«ΜώΒΟΝΥΗΟ100ΈΜΨ”Οώ‘¬Ψυ”ΟΥ°ΝΩΒΡΤΒ¬ Ζ÷≤Φ±μΘ§≤ΔΜφ÷ΤΝΥΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ®≤ΩΖ÷ ΐΨί“ΰ≤ΊΘ©
100ΈΜΨ”Οώ‘¬Ψυ”ΟΥ°ΝΩΒΡΤΒ¬ Ζ÷≤Φ±μ
ΉιΚ≈ | Ζ÷Ήι | ΤΒ ΐ | ΤΒ¬ |
1 |
| 4 | 0.04 |
2 |
| 0.08 | |
3 |
| 15 | |
4 |
| 22 | |
5 |
|
| |
6 |
| 14 | 0.14 |
7 |
| 6 |
|
8 |
| 4 | 0.04 |
9 |
| 0.02 | |
Κœ ΦΤ | 100 | ||

Θ®1Θ©»ΖΕ®±μ÷–![]() ”κ
”κ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©«σΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Ήσ ΐΒΎ4ΗωΨΊ–ΈΒΡΗΏΕ»ΘΜ
Θ®3Θ©‘ΎΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Μ≠≥ωΤΒ¬ Ζ÷≤Φ’έœΏΆΦΘΜ
Θ®4Θ©Έ“Ο«œκΒΟΒΫΉήΧεΟήΕ»«ζœΏΘ§«κΜΊ¥πΈ“Ο«”ΠΗΟ‘θΟ¥ΉωΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©ΦϊΫβΈωΘΜΘ®4Θ©ΦϊΫβΈω.
ΘΜΘ®3Θ©ΦϊΫβΈωΘΜΘ®4Θ©ΦϊΫβΈω.
ΓΨΫβΈωΓΩΖ÷ΈωΘΚΘ®1Θ©”…ΤΒ¬ Ζ÷≤Φ±μ÷–ΤΒ ΐ”κΤΒ¬ ΒΡΕ‘”ΠΙΊœΒΘ§Ω…“‘«σ≥ω![]() ΘΜ
ΘΜ
Θ®2Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ±μ»ΖΕ®ΒΎ4ΗωΨΊ–ΈΒΡΤΒ¬ Θ§‘Ό”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΉίΉχ±ξΈΣ![]() Θ§»ΖΕ®ΒΎ4ΗωΨΊ–ΈΒΡΗΏΕ»ΘΜ
Θ§»ΖΕ®ΒΎ4ΗωΨΊ–ΈΒΡΗΏΕ»ΘΜ
Θ®3Θ©“ά¥Έ»ΓΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–ΟΩΉιΒΡ÷–ΒψΉχ±ξΘ§Ν§œΏΦ¥ΈΣΤΒ¬ Ζ÷≤Φ’έœΏΆΦΘΜ
Θ®4Θ©ΗυΨίΉήΧεΟήΕ»«ζœΏΒΡΧΊΒψΘ§Ω…“‘≤…”Ο‘ω¥σ―υ±Ψ»ίΝΩΘ§Φθ–ΓΉιΨύΒΡΖΫΖ®Θ§’β―υ’έœΏΆΦΜαΫ”ΫϋΙβΜ§«ζœΏ.
œξΫβΘΚΫβΘΚΘ®1Θ©ΗυΨίΤΒ¬ Ζ÷≤Φ±μ÷–ΤΒ ΐ”κΤΒ¬ ΒΡΕ‘”Π±»άΐΙΊœΒΘ§≤Ι»ΪΖ÷≤Φ±μΘΚ
ΉιΚ≈ | Ζ÷Ήι | ΤΒ ΐ | ΤΒ¬ |
2 |
| 8 | 0.08 |
3 |
| 15 | 0.15 |
4 |
| 22 | 0.22 |
5 |
|
| 0.25 |
7 |
| 6 |
|
9 |
| 2 | 0.02 |
Κœ ΦΤ | 100 | 1 | |
Υυ“‘Θ§![]() ΘΜ
ΘΜ
Θ®2Θ©“ρΈΣΉσ ΐΒΎ4ΗωΨΊ–ΈΕ‘”ΠΒΡΤΒ¬ ΈΣ0.22,
Εχ±μ÷–Ω…Ω¥ΒΫΉιΨύΈΣ0.5.
Υυ“‘ΥϋΒΡΗΏΕ»ΈΣ![]() ΘΜ
ΘΜ
Θ®3Θ©

Θ®ΥυΜ≠’έœΏΒΡΗς≤ΩΖ÷≤Μ «œΏΕΈ≤ΜΗχΖ÷Θ§ΥυΜ≠’έœΏ»ΓΒψ≤Μ «÷–ΒψΩέ2Ζ÷Θ§”–Εύ”ύΒΡœΏΕΈΩέ1ΓΣ2Ζ÷Θ©
Θ®4Θ©ΈΣΝΥΒΟΒΫΉήΧεΟήΕ»«ζœΏΘ§Έ“Ο«Ω…“‘»Ο―υ±ΨΒΡ»ίΝΩ‘ωΦ”Θ§ΥυΖ÷ΒΡΉι‘ωΦ”Θ§ΉιΨύΦθ–ΓΘ§œύ”ΠΒΡΤΒ¬ ’έœΏΆΦΜα”ζά¥”ζΫ”Ϋϋ”Ύ“ΜΧθΙβΜ§ΒΡ«ζœΏΘ§Φ¥ΈΣΉήΧεΟήΕ»«ζœΏ.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
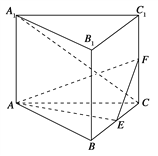
ΓΨΧβΡΩΓΩ(2015ΓΛΚΰΡœ)»γœ¬ΆΦΘ§÷±»ΐάβ÷υABCΘ≠A1B1C1ΒΡΒΉΟφ «±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§EΓΔFΖ÷±π «BCΓΔCC1ΒΡ÷–Βψ.
(1)÷ΛΟςΘΚΤΫΟφAEFΓΆΤΫΟφB1BCC1ΘΜ
(2)»τ÷±œΏA1C”κΤΫΟφA1ABB1Υυ≥…ΒΡΫ«ΈΣ45ΓψΘ§«σ»ΐάβΉΕFΘ≠AECΒΡΧεΜΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ Ψ≥Χ–ρΩρΆΦ «”ΟΓΑΕΰΖ÷Ζ®Γ±«σΖΫ≥Χ![]() ΒΡΫϋΥΤΫβΒΡΥψΖ®Θ§”–œ¬Ν–≈–ΕœΘΚ
ΒΡΫϋΥΤΫβΒΡΥψΖ®Θ§”–œ¬Ν–≈–ΕœΘΚ
ΔΌ»τ![]() ‘ρ δ≥ωΒΡ÷Β‘Ύ
‘ρ δ≥ωΒΡ÷Β‘Ύ![]() ÷°ΦδΘΜ
÷°ΦδΘΜ
ΔΎ»τ![]() ‘ρ≥Χ–ρ÷¥––Άξ±œΫΪΟΜ”–÷Β δ≥ωΘΜ
‘ρ≥Χ–ρ÷¥––Άξ±œΫΪΟΜ”–÷Β δ≥ωΘΜ
Δέ»τ![]() ‘ρ≥Χ–ρΩρΆΦΉνœ¬ΟφΒΡ≈–ΕœΩρΗ’ΚΟ÷¥––8¥Έ≥Χ–ρΨΆΫα χ.
‘ρ≥Χ–ρΩρΆΦΉνœ¬ΟφΒΡ≈–ΕœΩρΗ’ΚΟ÷¥––8¥Έ≥Χ–ρΨΆΫα χ.
Τδ÷–’ΐ»ΖΟϋΧβΒΡΗω ΐΈΣΘ® Θ©

A. 0 B. 1 C. 2 D. 3
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§A,B,C,DΕΦ‘ΎΆ§“ΜΗω”κΥ°ΤΫΟφ¥Ι÷±ΒΡΤΫΟφΡΎΘ§BΘ§DΈΣΝΫΒΚ…œΒΡΝΫΉυΒΤΥΰΒΡΥΰΕΞΓΘ≤βΝΩ¥§”ΎΥ°ΟφA¥Π≤βΒΟBΒψΚΆDΒψΒΡ―ωΫ«Ζ÷±πΈΣ![]() Θ§
Θ§![]() Θ§”ΎΥ°ΟφC¥Π≤βΒΟBΒψΚΆDΒψΒΡ―ωΫ«ΨυΈΣ
Θ§”ΎΥ°ΟφC¥Π≤βΒΟBΒψΚΆDΒψΒΡ―ωΫ«ΨυΈΣ![]() Θ§AC=0.1kmΓΘ
Θ§AC=0.1kmΓΘ

Θ®ΔώΘ© ‘ΧΫΨΩΆΦ÷–BΘ§DΦδΒΡΨύάκ”κΝμΆβΡΡΝΫΒψΦδΨύάκΜαœύΒ»ΘΩ
Θ®IIΘ©«σBΘ§DΦδΒΡΨύάκΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®ΔώΘ©“―÷Σx2+y2=1Θ§«σ2x+3yΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®ΔρΘ©“―÷Σa2+b2+c2©¹2a©¹2b©¹2c=0Θ§«σ÷ΛΘΚ ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣœρΝΩ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ®mΘΨ0Θ§nΘΨ0Θ©Θ§»τm+nΓ [1Θ§2]Θ§‘ρ
Θ®mΘΨ0Θ§nΘΨ0Θ©Θ§»τm+nΓ [1Θ§2]Θ§‘ρ ![]() ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
ΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣpΘΚxΓ A={x|x2©¹2x©¹3Γή0Θ§xΓ R}Θ§qΘΚxΓ B={x|x2©¹2mx+m2©¹9Γή0Θ§xΓ RΘ§mΓ R}Θ°
Θ®1Θ©»τAΓ…B=[1Θ§3]Θ§«σ Β ΐmΒΡ÷ΒΘΜ
Θ®2Θ©»τp «qΒΡ≥δΖ÷ΧθΦΰΘ§«σ Β ΐmΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏl1ΘΚaxΘΪbyΘΪ1ΘΫ0(aΘ§b≤ΜΆ§ ±ΈΣ0)Θ§l2ΘΚ(aΘ≠2)xΘΪyΘΪaΘΫ0Θ§
(1)»τbΘΫ0Θ§«“l1ΓΆl2Θ§«σ Β ΐaΒΡ÷ΒΘΜ
(2)Β±bΘΫ3Θ§«“l1ΓΈl2 ±Θ§«σ÷±œΏl1”κl2÷°ΦδΒΡΨύάκΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…η ΐΝ–![]() ΒΡ«Α
ΒΡ«Α![]() œνΚΆΈΣ
œνΚΆΈΣ![]() Θ§“―÷Σ
Θ§“―÷Σ![]() Θ®
Θ®![]() Θ©Θ§«“
Θ©Θ§«“![]() .
.
Θ®1Θ©÷ΛΟς![]() ΈΣΒ»±» ΐΝ–Θ§≤Δ«σ ΐΝ–
ΈΣΒ»±» ΐΝ–Θ§≤Δ«σ ΐΝ–![]() ΒΡΆ®œνΙΪ ΫΘΜ
ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…η![]() Θ§«“
Θ§«“![]() ÷ΛΟς
÷ΛΟς![]() ΘΜ
ΘΜ
Θ®3Θ©‘ΎΘ®2Θ©–ΓΈ ΒΡΧθΦΰœ¬Θ§»τΕ‘»Έ“βΒΡ![]() Θ§≤ΜΒ» Ϋ
Θ§≤ΜΒ» Ϋ![]() Κψ≥…ΝΔΘ§ ‘«σ Β ΐ
Κψ≥…ΝΔΘ§ ‘«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com