Question

【题目】已知等差数列{an}中，a2=6，a3+a6=27．
（1）求数列{an}的通项公式；
（2）记数列{an}的前n项和为Sn ， 且Tn= ，若对于一切正整数n，总有Tn≤m成立，求实数m的取值范围．

Answer 1

【答案】
（1）解：设等差数列{an}的公差为d，

由a2=6，a3+a6=27．可得a1+d=6，2a1+7d=27，

解得a1=d=3，

即有an=a1+（n﹣1）d=3n

（2）解：Tn= = = ，

Tn+1= ，

由 = ，

可得T1＜T2≤T3＞T4＞T5＞…＞Tn＞…

即有T2=T3= ，取得最大值．

对于一切正整数n，总有Tn≤m成立，

则有m≥ ．

即有m的取值范围是[ ，+∞）

【解析】（1）设等差数列{an}的公差为d，运用等差数列的通项公式，计算即可得到；（2）由等差数列的求和公式和数列的单调性，可得Tn的最大值，再由恒成立思想，即可得到m的范围．

【考点精析】本题主要考查了等差数列的前n项和公式和数列的前n项和的相关知识点，需要掌握前n项和公式：；数列{an}的前n项和sn与通项an的关系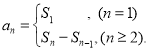才能正确解答此题．