
 如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:
如图,ABCD是正方形,SA⊥平面ABCD,BK⊥SC于点K,连接DK,求证:分析 (1)连接AC,由已知推导出BD⊥平面SAC,从而SC⊥平面KBD,由此能证明平面SBC⊥平面KBD.
(2)假设平面SBC⊥平面SDC,由已知推导出AB⊥SB,这与∠SBA是Rt△SAB的一个锐角矛盾,故假设不成立,从而得到平面SBC不垂直于平面SDC.
解答 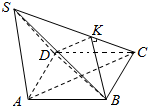 证明:(1)连接AC,∵四边形ABCD是正方形,
证明:(1)连接AC,∵四边形ABCD是正方形,
∴AC⊥BD.又SA⊥平面ABCD,∴SA⊥BD,
∴BD⊥平面SAC,∴SC⊥BD.
又∵SC⊥BK,∴SC⊥平面KBD.
又SC?平面SBC,∴平面SBC⊥平面KBD.
(2)假设平面SBC⊥平面SDC.
∵BK⊥SC,∴BK⊥平面SDC.
∵DC?平面SDC,∴BK⊥DC,
又AB∥CD,∴BK⊥AB.
∵ABCD是正方形,AB⊥BC,
∴AB⊥平面SBC,又SB?平面SBC,
∴AB⊥SB,这与∠SBA是Rt△SAB的一个锐角矛盾,故假设不成立.
∴原结论成立,即平面SBC不垂直于平面SDC.
点评 本题考查面面垂直的证明,考查平面不垂直的证明,是中档题,解题时要注意反证法的合理运用,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{2π+1}{3}$ | B. | $\frac{2π+3}{3}$ | C. | $\frac{4π+1}{3}$ | D. | $\frac{4π+3}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.
如图,已知瞭望塔BA的高度为40m,为测得古塔DC的高度,在B处望占塔的顶部,仰角是60°,在A处再次望古塔的顶部,仰角为45°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2 | B. | 1:$\sqrt{3}$ | C. | 1:$\sqrt{5}$ | D. | $\sqrt{3}$:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com