
分析 设F(x)=f(x)-(2x+7),则F′(x)=f′(x)-2,由对任意x∈R总有f′(x)>2,知F′(x)=f′(x)-2>0,所以F(x)=f(x)-2x-7在R上是增函数,由此能够求出结果.
解答 解:设F(x)=f(x)-(2x+7)=f(x)-2x-7,
则F′(x)=f′(x)-2,
∵f′(x)>2,
∴F′(x)=f′(x)-2>0,
∴F(x)=f(x)-2x-7在R上递增,
∵f(-3)=1,
∴F(-3)=f(-3)-2×(-3)-7=0,
∵f(x)<2x+7,
∴F(x)=f(x)-2x-7<0,
∴x<-3,
故答案为:(-∞,-3).
点评 本题考查利用导数研究函数的单调性的应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
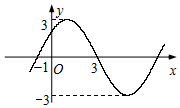 函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))的图象,如图所示,则f(2016)的值为$\frac{{3\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
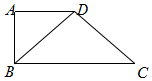 如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将
如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将| A. | 面ABD⊥面ABC | B. | 面ADC⊥面BDC | C. | 面ABC⊥面BDC | D. | 面ADC⊥面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com