
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:
| 视力数据 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 | 5.1 | 5.2 | 5.3 |
| 人数 | | | | | 2 | | 2 | | 2 | 1 | | 1 | | |
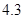 、
、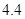 、
、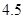 、
、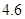 、
、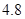 .若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于
.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于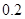 的概率.
的概率. (1)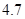 ;(2)
;(2)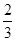 .
.
解析试题分析:(1)将样本数据取出来,分别记为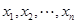 ,然后利用样本平均数计算公式
,然后利用样本平均数计算公式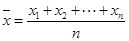 即可计算样本数据的平均数;(2)先将样本视力的平均数对用列举法表示出来,然后在选取符合条件的视力的平均数,最后利用古典概型的概率计算公式即可计算。
即可计算样本数据的平均数;(2)先将样本视力的平均数对用列举法表示出来,然后在选取符合条件的视力的平均数,最后利用古典概型的概率计算公式即可计算。
试题解析:(1)高三文科(1)班抽取的8名学生视力的平均值为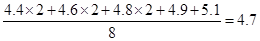 .
.
据此估计高三文科(1)班学生视力的平均值约为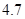 . 3分
. 3分
(2)因为高三文科六个班学生视力的平均值分别为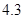 、
、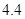 、
、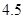 、
、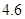 、
、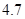 、
、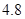 ,
,
所以任意抽取两个文科班学生视力的平均值数对有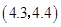 ,
,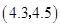 ,
,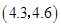 ,
,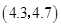 ,
,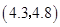 ,
, ,
,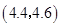 ,
,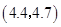 ,
,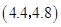 ,
, ,
,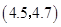 ,
,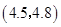 ,
,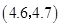 ,
,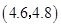 ,
,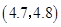 ,共15种情形. 7分
,共15种情形. 7分
其中抽取的两个班学生视力的平均值之差的绝对值不小于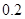 的有
的有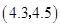 ,
,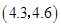 ,
,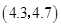 ,
, 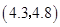 ,
,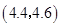 ,
,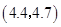 ,
,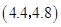 ,
,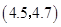 ,
,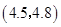 ,
,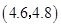 ,共10种.
,共10种.
10分
所以抽取的两个班学生视力的平均值之差的绝对值不小于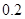 的概率为
的概率为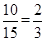 . 12分
. 12分
考点:样本的平均数计算,古典概型的概率计算


科目:高中数学 来源: 题型:解答题
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 3 | 5 | 7 | 7 | 5 | 3 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
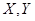 表示售出A、B商品的日利润值(单位:元).将频率视为概率.
表示售出A、B商品的日利润值(单位:元).将频率视为概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
| 组别 | 候车时间 | 人数 |
| 一 | 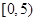 | 2 |
| 二 | 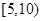 | 6 |
| 三 | 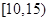 | 4 |
| 四 | 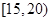 | 2 |
| 五 | 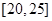 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有一条的为第一层,有二条的为第二层, ,依次类推.现有一颗小弹子从第一层的通道里向下运动,若在通道的分叉处,小弹子以相同的概率落入每个通道.记小弹子落入第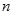 层第
层第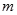 个竖直通道(从左至右)的概率为
个竖直通道(从左至右)的概率为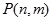 ,某研究性学习小组经探究发现小弹子落入第
,某研究性学习小组经探究发现小弹子落入第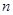 层的第
层的第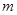 个通道的次数服从二项分布,请你解决下列问题.
个通道的次数服从二项分布,请你解决下列问题.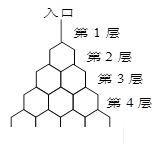
(Ⅰ)试求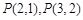 及
及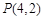 的值,并猜想
的值,并猜想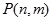 的表达式;(不必证明)
的表达式;(不必证明)
(Ⅱ)设小弹子落入第6层第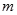 个竖直通道得到分数为
个竖直通道得到分数为 ,其中
,其中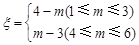 ,试求
,试求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲乙丙三人商量周末去玩,甲提议去市中心逛街,乙提议去城郊觅秋,丙表示随意。最终,商定以抛硬币的方式决定结果。规则是:由丙抛掷硬币若干次,若正面朝上则甲得一分乙得零分,反面朝上则乙得一分甲得零分,先得4分者获胜,三人均执行胜者的提议.记所需抛币次数为 .
.
⑴求 =6的概率;
=6的概率;
⑵求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系
位学生,每次活动均需该系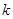 位学生参加(
位学生参加( 和
和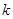 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系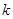 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使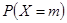 取得最大值的整数
取得最大值的整数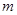 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com