
【题目】已知函数![]() ,
,
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)求函数![]() 的极值.
的极值.
【答案】(1)![]() 时,
时, ![]() 递减;
递减; ![]() 时,
时, ![]() 递增.
递增.
(2)见解析.
【解析】分析:(1)将![]() 代入函数
代入函数![]() 中,求导得
中,求导得![]() ,令
,令![]() 可得函数的单调递增区间,令
可得函数的单调递增区间,令![]() 可得函数的单调递减区间;(2)求导可得
可得函数的单调递减区间;(2)求导可得![]() ,对参数
,对参数![]() 分
分![]() 三种情况进行讨论,判断每种情况下
三种情况进行讨论,判断每种情况下![]() 的正负,进而可得函数
的正负,进而可得函数![]() 的增减性,得其极值情况.
的增减性,得其极值情况.
详解: (1)函数![]() 的定义域为
的定义域为![]() ,其导数为
,其导数为 ![]()
![]()
.当![]() 时,
时, ![]()
设![]() ,则
,则![]() ,显然
,显然![]() 时
时![]() 递增;
递增;
![]() 时,
时, ![]() 递减/span>,故
递减/span>,故![]() ,于是
,于是![]() ,
,
所以![]() 时,
时, ![]() 递减;
递减; ![]() 时,
时, ![]() 递增;
递增;
(2)由(1)知, ![]()
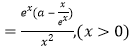 .
.
函数![]() 在
在![]() 递增在
递增在![]() 递减所以
递减所以![]()
又当![]() 时,
时, ![]() ,
,
①当![]() 时,
时, ![]() ,此时;
,此时;
因为![]() 时,
时, ![]() 递增;
递增; ![]() 时,
时, ![]() 递减;
递减;
所以![]() 无极小值;
无极小值;
②当![]() 时,
时,![]() ,此时;
,此时;
因为![]() 时,
时,![]() 递减;
递减;![]() 时.
时.![]() 递增;
递增;
所以![]() ,无极大值;
,无极大值;
③当![]() 时,
时,![]()
又![]() 在
在![]() 递增所以
递增所以![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,且
,且![]() .
.
易证: ![]() 时,
时, ![]() ,所以
,所以![]() ,
,
所以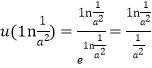
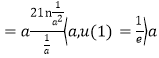
又![]() 在
在![]() 递减,所以
递减,所以![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,且
,且![]() ,故:
,故:
当![]() 时,
时, ![]() 递减;当
递减;当![]() ,
, ![]() 递增;
递增;
当![]() 时,
时, ![]() 递减;当
递减;当![]() ,
, ![]() 递增;
递增;
所以, ![]() ,
, ![]()
![]() ,
,
![]()
![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.先把高二年级的2000名学生编号:1到2000,再从编号为1到50的学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() ,……的学生,这种抽样方法是系统抽样法.
,……的学生,这种抽样方法是系统抽样法.
B.一组数据的方差为![]() ,平均数为
,平均数为![]() ,将这组数据的每一个数都乘以2,所得的一组新数据的方差和平均数为
,将这组数据的每一个数都乘以2,所得的一组新数据的方差和平均数为![]() ,
,![]() .
.
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1.
的值越接近于1.
D.若一组数据1,![]() ,3的平均数是2,则该组数据的方差是
,3的平均数是2,则该组数据的方差是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() .
.
①设直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,求
,求![]() 的取值范围;
的取值范围;
②求与动直线![]() 恒相切的定椭圆
恒相切的定椭圆![]() 的方程;并探究:若
的方程;并探究:若![]() 是曲线
是曲线![]() :
: ![]() 上的动点,是否存在直线
上的动点,是否存在直线![]() :
: ![]() 恒相切的定曲线
恒相切的定曲线![]() ?若存在,直接写出曲线
?若存在,直接写出曲线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐代卖店代售多种类型的快餐,深受广大消费者喜爱.其中,![]() 种类型的快餐每份进价为
种类型的快餐每份进价为![]() 元,并以每份
元,并以每份![]() 元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以
元的价格销售.如果当天20:00之前卖不完,剩余的该种快餐每份以![]() 元的价格作特价处理,且全部售完.
元的价格作特价处理,且全部售完.
(1)若该代卖店每天定制![]() 份
份![]() 种类型快餐,求
种类型快餐,求![]() 种类型快餐当天的利润
种类型快餐当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:份,
(单位:份,![]() )的函数解析式;
)的函数解析式;
(2)该代卖店记录了一个月![]() 天的
天的![]() 种类型快餐日需求量(每天20:00之前销售数量)
种类型快餐日需求量(每天20:00之前销售数量)
日需求量 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
(i)假设代卖店在这一个月内每天定制![]() 份
份![]() 种类型快餐,求这一个月
种类型快餐,求这一个月![]() 种类型快餐的日利润(单位:元)的平均数(精确到
种类型快餐的日利润(单位:元)的平均数(精确到![]() );
);
(ii)若代卖店每天定制![]() 份
份![]() 种类型快餐,以
种类型快餐,以![]() 天记录的日需求量的频率作为日需求量发生的概率,求
天记录的日需求量的频率作为日需求量发生的概率,求![]() 种类型快餐当天的利润不少于
种类型快餐当天的利润不少于![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 是公差为2的等差数列,数列
是公差为2的等差数列,数列![]() 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]()
对一切n∈N*恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() .
.
(1)求证:无论![]() 取何值,直线
取何值,直线![]() 始终经过第一象限;
始终经过第一象限;
(2)若直线![]() 与
与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴正半轴交于
轴正半轴交于![]() 点,
点,![]() 为坐标原点,设
为坐标原点,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且当
,且当![]() 时,
时,![]() 的最小值为2,
的最小值为2,
(1)求![]() 的值,并求
的值,并求![]() 的单调递增区间.
的单调递增区间.
(2)若将函数![]() 的图象上的点的纵坐标不变,横坐标缩小到原来的
的图象上的点的纵坐标不变,横坐标缩小到原来的![]() ,再将所得的图象向右平移
,再将所得的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求方程
的图象,求方程![]() 在区间
在区间![]() 上所有根之和.
上所有根之和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com