
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间与最值;
的单调区间与最值;
(2)若方程![]() 在区间
在区间![]() 内有两个不相等的实根,求实数
内有两个不相等的实根,求实数![]() 的取值范围.(其中
的取值范围.(其中![]() 为自然对数的底数)
为自然对数的底数)
科目:高中数学 来源: 题型:
【题目】设集合A,B是R中两个子集,对于![]() ,定义:
,定义: 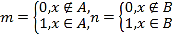 .①若
.①若![]() ;则对任意
;则对任意![]() ;②若对任意
;②若对任意![]() ,则
,则![]() ;③若对任意
;③若对任意![]() ,则A,B的关系为
,则A,B的关系为![]() .上述命题正确的序号是______. (请填写所有正确命题的序号)
.上述命题正确的序号是______. (请填写所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形![]() 与等腰直角三角形
与等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]() ,
,![]() ,
,![]() ,
,![]() .
.
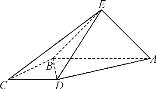
(1) 求证:![]() ;
;
(2) 求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]()
![]() 若存在,求出
若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列四个命题中,其中真命题是( )
①“若![]() ,则
,则![]() ”的逆命题;
”的逆命题;
②“若![]() ,则
,则![]() ”的否命题;
”的否命题;
③“若![]() ,则方程
,则方程![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“等边三角形的三个内角均为![]() ”的逆命题.
”的逆命题.
A. ①② B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
A.a<0B.a≤0C.a≤1D.a≤0或a=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系![]() 自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
(2)某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0.01%,若初始时含杂质0.2%,每次过滤可使杂质含量减少三分之一,问至少应过滤几次才能使得这种液体达到要求?(已知![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
(1)请将上面的列联表补充完整;
(2)能否在犯错概率不超过![]() 的前提下认为喜好体育运动与性别有关?说明你的理由.
的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式: ![]() )
)
临界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
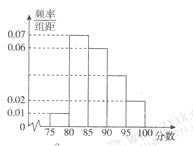
【题目】某高中在今年的期末考试历史成绩中随机抽取![]() 名考生的笔试成绩,作出其频率分布直方图如图所示,已知成绩在
名考生的笔试成绩,作出其频率分布直方图如图所示,已知成绩在![]() 中的学生有1名,若从成绩在
中的学生有1名,若从成绩在![]() 和
和![]() 两组的所有学生中任取2名进行问卷调查,则2名学生的成绩都在
两组的所有学生中任取2名进行问卷调查,则2名学生的成绩都在![]() 中的概率为( )
中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com