
【题目】设椭圆E: ![]() (a>b>0)的左、右焦点F1、F2 , 其离心率e=
(a>b>0)的左、右焦点F1、F2 , 其离心率e= ![]() ,且点F2到直线
,且点F2到直线 ![]() =1的距离为
=1的距离为 ![]() .
.
(1)求椭圆E的方程;
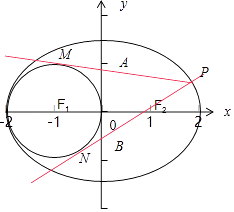
(2)设点P(x0 , y0)是椭圆E上的一点(x0≥1),过点P作圆(x+1)2+y2=1的两条切线,切线与y轴交于A、B两点,求|AB|的取值范围.
【答案】
(1)
解:设F1(﹣c,0),F2(c,0),
依题意有 ![]() ,
, ![]() .
.
又∵a2=b2+c2,∴c=1,a=2,b= ![]() ,
,
∴椭圆E的方程为: ![]() .
.
(2)
解:如图设圆的切线PM的方程为y=k(x﹣x0)+y0
由圆心(﹣1,0)到PM的距离为1,
|y0﹣k(x0+1)|= ![]() (x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0
(x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0
令y=k(x﹣x0)+y0中x=0,y=y0﹣kx0
∴A(0,y0﹣kx0).
设圆的切线PN的方程为y=k1(x﹣x0)+y0.
同理可得B(0,y0﹣k1x0)
依题意k1,k是方程(x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0的两个实根,
k1+k= ![]() ,k1k=
,k1k= ![]()
|AB|2=[x0(k﹣k1)]2= ![]() =
= ![]() .
.
∵ ![]() ,∴|AB|2=1+
,∴|AB|2=1+ ![]() =1+
=1+ ![]()
∵1≤x0≤2,∴|AB|2=1+ ![]() .
.
∴|AB|的取值范围为[ ![]() ]
]
【解析】(1)设F1(﹣c,0),F2(c,0),依题意有 ![]() ,
, ![]() .可得c=1,a=2,b=
.可得c=1,a=2,b= ![]() , (2)如图设圆的切线PM的方程为y=k(x﹣x0)+y0 , 由圆心(﹣1,0)到PM的距离为1,|y0﹣k(x0+1)|=
, (2)如图设圆的切线PM的方程为y=k(x﹣x0)+y0 , 由圆心(﹣1,0)到PM的距离为1,|y0﹣k(x0+1)|= ![]() (x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0,A(0,y0﹣kx0).设圆的切线PN的方程为y=k1(x﹣x0)+y0 , 同理可得B(0,y0﹣k1x0),依题意k1 , k是方程(x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0的两个实根,|AB|2=[x0(k﹣k1)]2=
(x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0,A(0,y0﹣kx0).设圆的切线PN的方程为y=k1(x﹣x0)+y0 , 同理可得B(0,y0﹣k1x0),依题意k1 , k是方程(x02+2x0)k2﹣2y0(x0+1)k+y02﹣1=0的两个实根,|AB|2=[x0(k﹣k1)]2= ![]() =
= ![]() .由
.由 ![]() ,得|AB|2=1+
,得|AB|2=1+ ![]() =1+
=1+ ![]() .
.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴非负半轴上,半径为2的圆C与直线
轴非负半轴上,半径为2的圆C与直线![]() 相切.
相切.
(1)求圆C的方程;
(2)设不过原点O的直线l与圆O:x2+y2=4相交于不同的两点A,B.①求△OAB的面积的最大值;②在圆C上,是否存在点M(m,n),使得直线l的方程为mx+ny=1,且此时△OAB的面积恰好取到①中的最大值?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.命题“?x0∈R,x02﹣x0≤0”的否定为“?x∈R,x2﹣x>0”
B.命题“在△ABC中,A>30°,则sinA> ![]() ”的逆否命题为真命题
”的逆否命题为真命题
C.设{an}是公比为q的等比数列,则“q>1”是“{an}为递增数列”的充分必要条件
D.若非零向量 ![]() 、
、 ![]() 满足|
满足| ![]() +
+ ![]() |=|
|=| ![]() |+|
|+| ![]() |,则
|,则 ![]() 与
与 ![]() 共线
共线
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,O为坐标原点.动点P在圆
中,O为坐标原点.动点P在圆![]() 上,过P作y轴的垂线,垂足为N,点M在射线NP上,满足
上,过P作y轴的垂线,垂足为N,点M在射线NP上,满足![]() .
.

(1)求点M的轨迹G的方程;
(2)过点![]() 的直线l交轨迹G 于A,B两点,交圆O于C,D两点.若
的直线l交轨迹G 于A,B两点,交圆O于C,D两点.若![]() ,求直线l的方程;
,求直线l的方程;
(3)设点Q(3, t)(t∈R,t ≠ 0),且![]() ,过点P且垂直于OQ的直线m与OQ交于点E,与x轴交于点F,求△OEF周长最大时的直线m的方程.
,过点P且垂直于OQ的直线m与OQ交于点E,与x轴交于点F,求△OEF周长最大时的直线m的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和Sn满足Sn=![]() ,且a1,a2+1,a3成等差数列.
,且a1,a2+1,a3成等差数列.
(1)求数列{an}的通项公式;
(2)记数列![]() 的前n项和为Tn,求证:
的前n项和为Tn,求证:![]() Tn<1.
Tn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣2ax(其中a∈R).
(Ⅰ)当a=1时,求函数f(x)的图象在x=1处的切线方程;
(Ⅱ)若f(x)≤1恒成立,求a的取值范围;
(Ⅲ)设g(x)=f(x)+ ![]() x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
x2 , 且函数g(x)有极大值点x0 , 求证:x0f(x0)+1+ax02>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过原点O(0,0)且与直线y=2x﹣8相切于点P(4,0).
(1)求圆C的方程;
(2)已知直线l经过点(4, 5),且与圆C相交于M,N两点,若|MN|=2,求出直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com