Question

【题目】如图，菱形ABCD的对角线AC与BD交于点O，点E，F分别在AD，CD上，AE＝CF，EF交BD于点H.将△DEF沿EF折到△D′EF的位置．

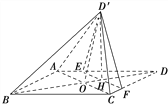
(1)证明：AC⊥HD′；

(2)若AB＝5，AC＝6，AE＝，OD′＝2，求五棱锥D′ABCFE的体积．

Answer 1

【答案】（1）详见解析（2）

【解析】试题分析：（1）折叠后仍有EF⊥HD，而AC∥EF，可得AC⊥HD′.（2）先定高线：OD′，由勾股定理得OD′⊥OH.由（1）得AC⊥OD′.因此OD′⊥平面ABC.再根据锥体体积公式求体积

试题解析：(1)证明：由已知得AC⊥BD，AD＝CD.

又由AE＝CF得＝，故AC∥EF.

由此得EF⊥HD，故EF⊥HD′，所以AC⊥HD′.

(2)由EF∥AC得.

由AB＝5，AC＝6得DO＝BO＝＝4.

所以OH＝1，D′H＝DH＝3.

于是OD′2＋OH2＝(2)2＋12＝9＝D′H2，

故OD′⊥OH.

由(1)知AC⊥HD′，又AC⊥BD，BD∩HD′＝H，

所以AC⊥平面BHD′，于是AC⊥OD′.

又由OD′⊥OH，AC∩OH＝O，所以OD′⊥平面ABC.

又由＝得EF＝.

五边形ABCFE的面积S＝×6×8－××3＝.

所以五棱锥D′ABCFE的体积V＝××2＝.

点睛:立体几何中折叠问题,要注重折叠前后垂直关系的变化,不变的垂直关系是解决问题的关键条件.