
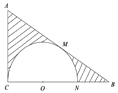
【题目】如图, △ABC 中, ACB 90 , ABC 30 , BC ![]() ,在三角形内挖去一个半圆(圆心 O 在边 BC 上,半圆与 AC,AB 分别相切于点 C,M ,与 BC 交于点 N ),将其绕直线 BC旋转一周得到一个旋转体,则该旋转体体积为________;
,在三角形内挖去一个半圆(圆心 O 在边 BC 上,半圆与 AC,AB 分别相切于点 C,M ,与 BC 交于点 N ),将其绕直线 BC旋转一周得到一个旋转体,则该旋转体体积为________;
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 长轴的两顶点为
长轴的两顶点为![]() 、
、![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,焦距为
,焦距为![]() ,且
,且![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线被椭圆
轴的直线被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在双曲线![]() 上取点
上取点![]() 异于顶点,直线
异于顶点,直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() 、
、![]() ,试证明:
,试证明:![]() 为定值;
为定值;
(3)在椭圆![]() 外的抛物线
外的抛物线![]() 上取一点
上取一点![]() ,若
,若![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+2|x+1|.
(1)当a=2时,解不等式f(x)>4.
(2)若不等式f(x)<3x+4的解集是{x|x>2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知四棱锥 P ABCD 的底面是边长为 6 的正方形,侧棱 PA 的长为 8,且垂直于底面,点 M . N 分别是 DC .AB 的中点。

求:(1)异面直线 PM 与 CN 所成角的正切值;
(2)四棱锥 P ABCD 的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆 C : ![]()
![]() ,称圆心在原点,半径为
,称圆心在原点,半径为![]() 的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(
的圆是椭圆 C 的“伴随圆”.若椭圆 C 的一个焦点为 F1(![]() , 0) ,其短轴上的一个端点到 F1 的距离为
, 0) ,其短轴上的一个端点到 F1 的距离为![]()
(1)求椭圆 C 的方程及其“伴随圆”方程;
(2)若倾斜角 45°的直线 l 与椭圆 C 只有一个公共点,且与椭圆 C 的伴随圆相交于 M .N 两点,求弦 MN 的的长;
(3)点 P 是椭圆 C 的伴随圆上一个动点,过点 P 作直线 l1、l2,使得 l1、l2与椭圆 C 都只有一个公共点,判断l1、l2的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保障全国第四次经济普查顺利进行,国家统计局从东部选择江苏,从中部选择河北. 湖北,从西部选择宁夏,从直辖市中选择重庆作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验.在某普查小区,共有 50 家企事业单位,150 家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 50 | |
个体经营户 | 50 | 150 | |
合计 |
(1)写出选择 5 个国家综合试点地区采用的抽样方法;
(2)补全上述列联表(在答题卡填写),并根据列联表判断是否有![]() 的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;
(3)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
附:![]()
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com