
【题目】定义“正对数”: ![]() ,现有四个命题:
,现有四个命题:
①若![]() ,则
,则![]()
②若![]() ,则
,则![]()
③若![]() ,则
,则![]()
④若![]() ,则
,则![]()
其中的真命题有:____________ (写出所有真命题的编号)
【答案】①③④
【解析】试题分析:
因为定义的“正对数”: ![]() 是一个分段函数 ,所以对命题的判断必须分情况讨论:
是一个分段函数 ,所以对命题的判断必须分情况讨论:
对于命题①(1)当![]() ,
, ![]() 时,有
时,有![]() ,从而
,从而![]() ,
, ![]() ,所以
,所以![]() ;(2)当
;(2)当![]() ,
, ![]() 时,有
时,有![]() ,从而
,从而![]() ,
, ![]() ,所以
,所以![]() ;这样若
;这样若![]() ,则
,则![]() ,即命题①正确.
,即命题①正确.
对于命题②举反例:当![]() 时,
时, ![]() ,
, ![]()
所以![]() ,即命题②不正确.
,即命题②不正确.
对于命题③,首先我们通过定义可知“正对数”有以下性质: ![]() ,且
,且![]() ,(1)当
,(1)当![]() ,
, ![]() 时,
时, ![]() ,而
,而![]() ,所以
,所以![]() ;(2)当
;(2)当![]() ,
, ![]() 时,有
时,有![]() ,
, ![]() ,而
,而![]() ,因为
,因为![]() ,所以
,所以![]() ;(3)当
;(3)当![]() ,
, ![]() 时,有
时,有![]() ,
, ![]() ,而
,而![]() ,所以
,所以![]() ;(4)当
;(4)当![]() ,
, ![]() 时,
时, ![]() ,而
,而![]() ,所以
,所以![]() ,综上即命题③正确.
,综上即命题③正确.
对于命题④首先我们通过定义可知“正对数”还具有性质:若![]() ,则
,则![]() ,(1)当
,(1)当![]() ,
, ![]() 时,有
时,有![]() ,从而
,从而![]() ,
, ![]() ,所以
,所以![]() ;(2)当
;(2)当![]() ,
, ![]() 时,有
时,有![]() ,从而
,从而![]() ,
, ![]() ,所以
,所以![]() ;(3)当
;(3)当![]() ,
, ![]() 时,与(2)同理,所以
时,与(2)同理,所以![]() ;(4)当
;(4)当![]() ,
, ![]() 时,
时, ![]() ,
, ![]() ,因为
,因为![]() ,所以
,所以![]() ,从而
,从而![]() ,综上即命题④正确.
,综上即命题④正确.
通过以上分析可知:真命题有①③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+)(A>0,ω>0)在x∈(0,7π)内取到一个最大值和一个最小值,且当x=π时,y有最大值3,当x=6π时,y有最小值﹣3.
(1)求此函数解析式;
(2)写出该函数的单调递增区间;
(3)是否存在实数m,满足不等式Asin( ![]() )>Asin(
)>Asin( ![]() )?若存在,求出m值(或范围),若不存在,请说明理由.
)?若存在,求出m值(或范围),若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)当a>0时,求函数f(x)的单调区间;
(2)若f(x)在[1,e]上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数);
(3)若 ![]() 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1
(1) 求数列{an}的通项公式;
(2) 设数列{bn}的前n项和Tn,且Tn+![]() = λ(λ为常数),令cn=b2n,(n∈N).求数列{cn}的前n项和Rn.
= λ(λ为常数),令cn=b2n,(n∈N).求数列{cn}的前n项和Rn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲、乙、丙、丁4个学生课余参加学校社团文学社与街舞社的活动,每人参加且只能参加一个社团的活动,且参加每个社团是等可能的.
(1)求文学社和街舞社都至少有1人参加的概率;
(2)求甲、乙同在一个社团,且丙、丁不同在一个社团的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在区间(﹣1,1)上的奇函数,且f(2)=
是定义在区间(﹣1,1)上的奇函数,且f(2)= ![]() ,
,
(1)确定函数f(x)的解析式;
(2)用定义法证明f(x)在区间(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() (a∈R),且f(1)>f(3),f(2)>f(3)( )
(a∈R),且f(1)>f(3),f(2)>f(3)( )
A.若k=1,则|a﹣1|<|a﹣2|
B.若k=1,则|a﹣1|>|a﹣2|
C.若k=2,则|a﹣1|<|a﹣2|
D.若k=2,则|a﹣1|>|a﹣2|
查看答案和解析>>
科目:高中数学 来源: 题型:
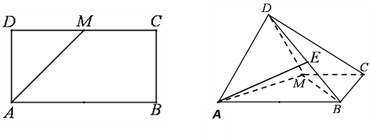
【题目】如图,已知长方形![]() 中,
中,![]() ,
, ![]() 为
为![]() 的中点。将
的中点。将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() 。
。
(1)求证:![]() ;
;
(2)若点![]() 是线段
是线段![]() 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角![]() 的余弦值为
的余弦值为![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com