
已知幂函数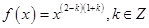 ,且
,且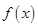 在
在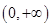 上单调递增.
上单调递增.
(1)求实数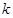 的值,并写出相应的函数
的值,并写出相应的函数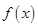 的解析式;
的解析式;
(2)若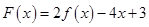 在区间
在区间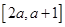 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(3)试判断是否存在正数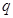 ,使函数
,使函数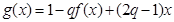 在区间
在区间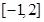 上的值域为
上的值域为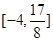 若存在,求出
若存在,求出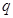 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) 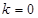 或
或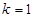 ,
,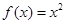 (2)
(2) 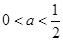 (3)
(3) 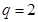
解析试题分析:(1)由题意知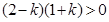 ,解得:
,解得: . 2分
. 2分
又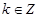 ∴
∴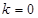 或
或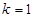 , 3分
, 3分
分别代入原函数,得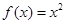 . 4分
. 4分
(2)由已知得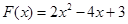 . 5分
. 5分
要使函数不单调,则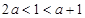 ,则
,则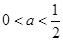 . 8分
. 8分
(3)由已知,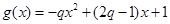 . 9分
. 9分
法一:假设存在这样的正数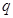 符合题意,
符合题意,
则函数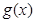 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为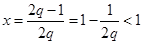 ,
,
因而,函数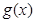 在
在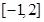 上的最小值只能在
上的最小值只能在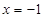 或
或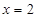 处取得,
处取得,
又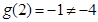 ,
,
从而必有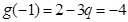 ,解得
,解得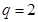 .
.
此时,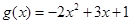 ,其对称轴
,其对称轴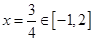 ,
,
∴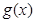 在
在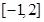 上的最大值为
上的最大值为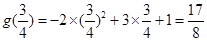 ,符合题意.
,符合题意.
∴存在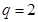 ,使函数
,使函数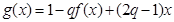 在区间
在区间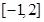 上的值域为
上的值域为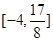 14分法二:假设存在这样的正数
14分法二:假设存在这样的正数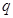 符合题意,
符合题意,
由(1)知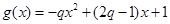 ,
,
则函数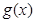 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为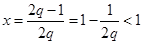 ,
,
考点:幂函数及二次函数单调性最值
点评:第二问中二次函数不单调需满足对称轴在给定区间内,第三问关于最值的考查需注意对称轴与给定区间的关系,从而确定给定区间上的单调性得到最值,一般求解时都要分情况讨论


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
已知函数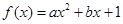 (
(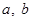 为实数,
为实数,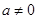 ,
,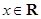 ),
),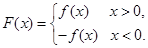
(Ⅰ)若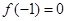 ,且函数
,且函数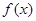 的值域为
的值域为 ,求
,求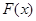 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当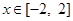 时,
时, 是单调函数,求实数
是单调函数,求实数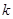 的取值范围;
的取值范围;
(Ⅲ)设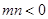 ,
,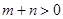 ,
,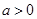 ,且函数
,且函数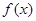 为偶函数,判断
为偶函数,判断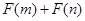 是否大于
是否大于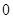 ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人2002年底花100万元买了一套住房,其中首付30万元,70万元采用商业贷款.贷款的月利率为5‰,按复利计算,每月等额还贷一次,10年还清,并从贷款后的次月开始还贷.
(1)这个人每月应还贷多少元?
(2)为了抑制高房价,国家出台“国五条”,要求卖房时按照差额的20%缴税.如果这个人现在将住房150万元卖出,并且差额税由卖房人承担,问:卖房人将获利约多少元?(参考数据:(1+0.005)120≈1.8)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时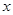 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米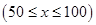 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油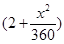 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(Ⅰ)求这次行车总费用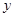 关于
关于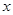 的表达式;
的表达式;
(Ⅱ)当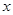 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
江苏某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为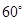 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为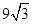 平方米,且高度不低于
平方米,且高度不低于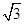 米,设防洪堤横断面的腰长为
米,设防洪堤横断面的腰长为 米,外周长(梯形的上底线段BC与两腰长的和)为
米,外周长(梯形的上底线段BC与两腰长的和)为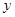 米.
米.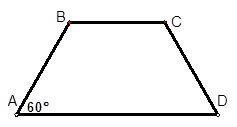
(1)求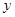 关于
关于 的函数关系式,并指出其定义域;
的函数关系式,并指出其定义域;
(2)要使防洪提的横断面的外周长不超过10.5米,则其腰长应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品在一个生产周期内的总产量为100t,平均分成若干批生产。设每批生产需要投入固定费用75元,而每批生产直接消耗的费用与产品数量x的平方成正比,已知每批生产10t时,直接消耗的费用为300元(不包括固定的费用)。
(1)若每批产品数量为20t,求此产品在一个生产周期的总费用(固定费用和直接消耗的费用)。
(2)设每批产品数量为xt,一个生产周期内的总费用y元,求y与x的函数关系式,并求
出y的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com