
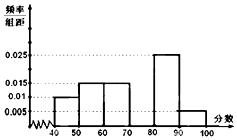
 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩(均为整数,满分100分)分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:分析 (1)先求出第四小组分数在[70,80)内的频率,由此能求出第四个小矩形的高.
(2)由题意求出60分以上的各组频率和,从而得到这次考试的及格率,由频率分布直方图能求出本次考试中的平均分.
(3)由已知可得C组共有学生人,从B,C两组共5人中选两人参加科普知识竞赛,设5人分别为B1,B2,C1,C2,C3,利用列举法能求出这两个学生都来自C组的概率.
解答 解:(1)第四小组分数在[70,80)内的频率为:
1-(0.005+0.01+0.015+0.015+0.025)×10=0.30,
∴第四个小矩形的高为:$\frac{0.30}{10}$=0.03 …(4分)
(2)由题意60分以上的各组频率和为:(0.015+0.03+0.025+0.005)×10=0.75,
故这次考试的及格率约为75%,…(6分)
由45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71,
得本次考试中的平均分约为71:…(8分)
(3)由已知可得C组共有学生60×10×0.005=3人,
则从B,C两组共5人中选两人参加科普知识竞赛,设5人分别为B1,B2,C1,C2,C3,
共有(B1,B2),(B1,C1),(B1,C2),(B1,C3),(B2,C1),
(B2,C2),(B2,C3),(C1,C2),(C1,C3),(C2,C3)等10种不同情况,
其中这两个学生都来自C组有3种不同情况,
∴这两个学生都来自C组的概率$P=\frac{3}{10}$. …(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
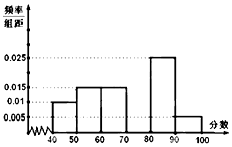 某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高二年级数学竞赛考试的学生中抽出60名学生,将其成绩分成六段,然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 7 | C. | 5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com