
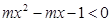 .
.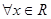 不等式恒成立,求实数
不等式恒成立,求实数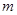 的取值范围;
的取值范围;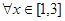 不等式恒成立,求实数
不等式恒成立,求实数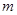 的取值范围;
的取值范围;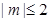 的一切m的值不等式恒成立,求实数
的一切m的值不等式恒成立,求实数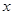 的取值范围.
的取值范围.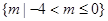 (2)
(2)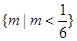 (3)
(3)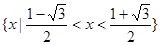
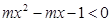 恒成立
恒成立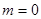 ,显然
,显然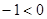 ……1分
……1分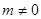 ,则
,则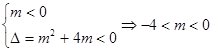 ……3分
……3分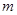 的取值范围是
的取值范围是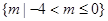 ……4分
……4分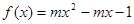
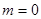 时,
时,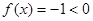 显然恒成立 ……5分
显然恒成立 ……5分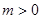 时,若对
时,若对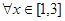 不等式恒成立,只需
不等式恒成立,只需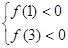 即可
即可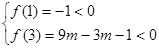 ,解得
,解得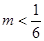 ……7分
……7分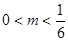 ……8分
……8分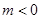 时,函数
时,函数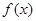 的图象开口向下,对称轴为
的图象开口向下,对称轴为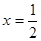 ,若对
,若对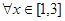 不等式恒成立,结合函数图象知只需
不等式恒成立,结合函数图象知只需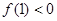 即可,解得
即可,解得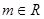
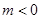 ……10分
……10分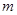 的取值范围是
的取值范围是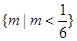 ……11分
……11分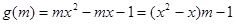
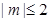 的一切m的值不等式恒成立,则只需
的一切m的值不等式恒成立,则只需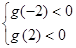 即可
即可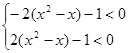 ,解得
,解得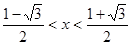 ……13分
……13分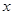 的取值范围是
的取值范围是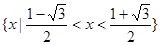 ……14分
……14分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com