
【题目】已知直线l1:x+my+6=0,l2:(m﹣2)x+3y+2m=0,求:
(1)若l1⊥l2 , 求m的值;
(2)若l1∥l2 , 求m的值.
【答案】
(1)解:由两直线垂直的充要条件可得:1(m﹣2)+m3=0,解得 ![]() ,
,
故当l1⊥l2时,m= ![]()
(2)解:由平行的条件可得: ![]() ,
,
由 ![]() 解得:m=﹣1或m=3;
解得:m=﹣1或m=3;
而当m=3时,l1与l2重合,不满足题意,舍去,故m=﹣1
【解析】(1)由两直线垂直的充要条件可得:1(m﹣2)+m3=0,解之即可;(2)由平行的条件可得: ![]() ,解后注意验证.
,解后注意验证.
【考点精析】利用两条直线平行与倾斜角、斜率的关系和两条直线垂直与倾斜角、斜率的关系对题目进行判断即可得到答案,需要熟知两条直线都有斜率而且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,那么它们平行;两条直线都有斜率,如果它们互相垂直,那么它们的斜率互为负倒数;反之,如果它们的斜率互为负倒数,那么它们互相垂直.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为[0,10),[10,20),[20,30),[30,40),[40,50]. 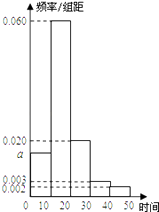
(1)求频率分布直方图中a的值;
(2)从统计学的角度说明学校是否需要推迟5分钟上课;
(3)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在[40,50]上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学生赵敏利用寒假参加社会实践,对机械销售公司7月份至12月份销售某种机械配件的销售量及销售单价进行了调查,销售单价![]() 和销售量
和销售量![]() 之间的一组数据如下表所示:
之间的一组数据如下表所示:
月份 | 7 | 8 | 9 | 10 | 11 | 12 |
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据7至11月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中 ,参考数据:
,参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
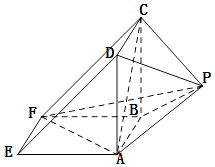
【题目】如图所示,该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成,AD⊥AF,AE=AD=2.
(Ⅰ)证明:平面PAD⊥平面ABFE;
(Ⅱ)求正四棱锥P﹣ABCD的高h,使得二面角C﹣AF﹣P的余弦值是 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若钝角三角形的三边长和面积都是整数,则称这样的三角形为“钝角整数三角形”,下列选项中能构成一个“钝角整数三角形”三边长的是( )
A.2,3,4
B.2,4,5
C.5,5,6
D.4,13,15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与
与![]() 相交于
相交于![]() 两点,求过
两点,求过![]() 两点且面积最小的圆的标准方程.
两点且面积最小的圆的标准方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com