
【题目】如图,在南北方向有一条公路,一半径为100![]() 的圆形广场(圆心为
的圆形广场(圆心为![]() )与此公路所在直线
)与此公路所在直线![]() 相切于点
相切于点![]() ,点
,点![]() 为北半圆弧(弧
为北半圆弧(弧![]() )上的一点,过点
)上的一点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,计划在
,计划在![]() 内(图中阴影部分)进行绿化,设
内(图中阴影部分)进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),
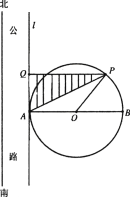
(1)设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
(2)确定点![]() 的位置,使绿化面积最大,并求出最大面积.
的位置,使绿化面积最大,并求出最大面积.
科目:高中数学 来源: 题型:
【题目】某校的![]() 名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取
名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取![]() 名学生的数学成绩(满分:
名学生的数学成绩(满分:![]() 分),并绘制成如图所示的茎叶图.将成绩低于
分),并绘制成如图所示的茎叶图.将成绩低于![]() 分的称为“不及格”,不低于
分的称为“不及格”,不低于![]() 分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.
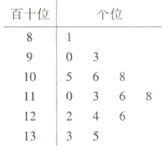
(1)估算此次联考该校高三学生的数学学科的平均成绩.
(2)估算此次联考该校高三学生数学成绩“不及格”和“优秀”的人数各是多少.
(3)在国家扶贫政策的倡导下,该地教育部门提出了教育扶贫活动,要求对此次数学成绩“不及格”的学生分两期进行学业辅导:一期由优秀学生进行一对一帮扶辅导,二期由老师进行集中辅导.根据实践总结,优秀学生进行一对一辅导的转化率为![]() ;老师集中辅导的转化率为
;老师集中辅导的转化率为![]() ,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.
注:转化率![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车零件加工厂为迎接国庆大促销活动预估国庆七天销售量,该厂工作人员根据以往该厂的销售情况,绘制了该厂日销售量的频率分布直方图,如图所示,将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
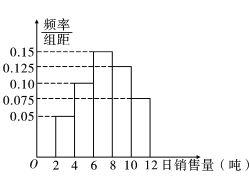
(1)根据频率分布直方图估计该厂的日平均销售量;(每组以中点值为代表)
(2)求未来![]() 天内,连续
天内,连续![]() 天日销售量不低于
天日销售量不低于![]() 吨,另一天日销售量低于
吨,另一天日销售量低于![]() 吨的概率;
吨的概率;
(3)用![]() 表示未来
表示未来![]() 天内日销售量不低于
天内日销售量不低于![]() 吨的天数,求随机变量
吨的天数,求随机变量![]() 的分布列、数学期望与方差.
的分布列、数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最近几年汽车金融公司发展迅猛,主要受益于监管层面对消费进人门槛的降低,互联网信贷消费的推广普及,以及汽车销售市场规模的扩张.如图是2013﹣2017年汽车金融行业资产规模统计图(单位:亿元).
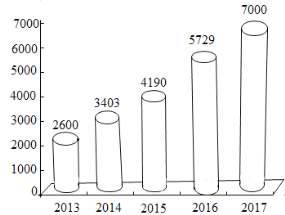
(1)以年份值2013,2014,…为横坐标,汽车金融行业资产规模(单位:亿元)为纵坐标,求y关于x的线性回归方程;
(2)利用(1)中的回归方程,预计2018年汽车金融行业资产规模(精确到亿元).
附:回归直线的斜率和截距的最小二乘估计公式分别为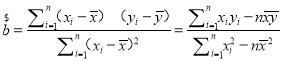 ,
,![]() (其中
(其中![]() ,
,![]() 为样本平均值).
为样本平均值).
参考数据:![]() 4.620×107,2015
4.620×107,2015![]() 4.619×107.
4.619×107.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是________(写出所有正确命题的编号)
①命题“若![]() ,则
,则![]() 且
且![]() ”的否定是“若
”的否定是“若![]() ,则
,则![]() 且
且![]() ”
”
②已知函数![]() 的图象关于直线
的图象关于直线![]() 对称,函数
对称,函数![]() 为奇函数,则4是
为奇函数,则4是![]() 一个周期.
一个周期.
③平面![]() ,
,![]() ,过
,过![]() 内一点
内一点![]() 作
作![]() 的垂线
的垂线![]() ,则
,则![]() .
.
④在![]() 中角
中角![]() 所对的边分别为
所对的边分别为![]() ,若
,若![]() ,则
,则![]() 成等差数列.
成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
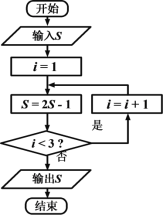
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.
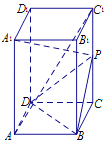
(1)求证:AC1∥平面PBD;
(2)求证:BD⊥A1P.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为真命题
均为真命题
C.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() |”
|”
D.若命题![]() ,使得
,使得![]() ,则
,则![]() ,恒有
,恒有![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com