
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 合 计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
合 计 | 60 | 50 | 110 |
根据上述数据能得出的结论是( )
(参考公式与数据:X2= ![]() .当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
.当X2>3.841时,有95%的把握说事件A与B有关;当X2>6.635时,有99%的把握说事件A与B有关; 当X2<3.841时认为事件A与B无关.)
A.有99%的把握认为“爱好该项运动与性别有关”
B.有99%的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C1: ![]() .
.
(1)求与双曲线C1有相同焦点,且过点P(4, ![]() )的双曲线C2的标准方程;
)的双曲线C2的标准方程;
(2)直线l:y=x+m分别交双曲线C1的两条渐近线于A、B两点.当 ![]()
![]() =3时,求实数m的值.
=3时,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() (ax﹣a﹣x)(a>0且a≠1).
(ax﹣a﹣x)(a>0且a≠1).
(1)判断f(x)的奇偶性.
(2)讨论f(x)的单调性.
(3)当x∈[﹣1,1]时,f(x)≥b恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆的参数方程为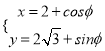 (
(![]() 为参数),以直角坐标系的原点为极点,
为参数),以直角坐标系的原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)将圆的参数方程化为普通方程,再化为极坐标方程;
(Ⅱ)若点![]() 在直线
在直线![]() 上,当点
上,当点![]() 到圆的距离最小时,求点
到圆的距离最小时,求点![]() 的极坐标.
的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+2)x+alnx.
(1)当a=1时,求函数f(x)的极值;
(2)设定义在D上的函数y=g(x)在点P(x0 , y0)处的切线方程为l:y=h(x).当x≠x0时,若 ![]() >0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,问函数y=f(x)是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
>0在D内恒成立,则称P为函数y=g(x)的“转点”.当a=8时,问函数y=f(x)是否存在“转点”?若存在,求出“转点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com