
分析 取AB,B1B的中点为M,D,连接DF,DM,ME,作EN⊥DF,垂足为N,则DM为EF在平面A1AB上的射影,EN∥MD,可得∠NEF为直线EF与平面A1AB所成角,即可得出结论.
解答  解:取AB,B1B的中点为M,D,连接DF,DM,ME,作EN⊥DF,垂足为N,则DM为EF在平面A1AB上的射影,EN∥MD,
解:取AB,B1B的中点为M,D,连接DF,DM,ME,作EN⊥DF,垂足为N,则DM为EF在平面A1AB上的射影,EN∥MD,
∴∠NEF为直线EF与平面A1AB所成角,
设AB=2a,则EN=$\sqrt{2}$a,EF=$\sqrt{3}$a,
∴直线EF与平面A1AB所成角的余弦值为$\frac{{\sqrt{6}}}{3}$.
故答案为:$\frac{{\sqrt{6}}}{3}$.
点评 本题考查直线EF与平面A1AB所成角的余弦值,考查学生的计算能力,正确确定直线EF与平面A1AB所成角是关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{6}}{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (-∞,2]∪[3,+∞) | C. | [-1,6] | D. | [-6,1] |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:解答题
已知动圆M与圆C1:(x+4)2+y2=2外切,与圆C2:(x-4)2+y2=2内切,求动圆圆心M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
若P是以F1,F2为焦点的椭圆 =1(a>b>0)上的一点,且
=1(a>b>0)上的一点,且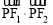 =0,tan∠PF1F2=
=0,tan∠PF1F2= ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二理上月考一数学理试卷(解析版) 题型:填空题
F1、F2是双曲线 -
- =1的两个焦点,P在双曲线上且满足|PF1|·|PF2|=
=1的两个焦点,P在双曲线上且满足|PF1|·|PF2|= ,则∠F1PF2=__________.
,则∠F1PF2=__________.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:解答题
如图1是图2的三视图,三棱锥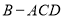 中,
中,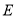 ,
, 分别是棱
分别是棱 ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com