
 .9和0.85.若预防方案允许甲乙两种方案单独采用、联合采用或不采用,请确定预防方案使总费用最少。(总费用=采取预防措施的费用+发生突发事件损失的期望值)
.9和0.85.若预防方案允许甲乙两种方案单独采用、联合采用或不采用,请确定预防方案使总费用最少。(总费用=采取预防措施的费用+发生突发事件损失的期望值) .15=60(万元),总费用为30+60=90(万元);
.15=60(万元),总费用为30+60=90(万元); ,比较其总费用可知,应选择联合采用甲、乙两种预防措施,可使总费用最少。
,比较其总费用可知,应选择联合采用甲、乙两种预防措施,可使总费用最少。

 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源:不详 题型:单选题
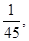 则该单位员工总数为
则该单位员工总数为 | A.110 | B.100 | C.90 | D.80 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 试分别求出系统甲、乙能正常工作的概率p1,p2;
试分别求出系统甲、乙能正常工作的概率p1,p2;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 排放量超过
排放量超过 的
的 型新车进行惩罚.某检测单位对甲、乙两类
型新车进行惩罚.某检测单位对甲、乙两类 型品牌车各抽取
型品牌车各抽取 辆进行
辆进行 排放量检测,记录如下(单位:
排放量检测,记录如下(单位: ).
).| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | 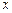 |  | 160 |
 排放量的平均值为
排放量的平均值为
 .
. 排放量的概率是多少?
排放量的概率是多少? ,试比较甲、乙两类品牌车
,试比较甲、乙两类品牌车 排放量的稳定性.
排放量的稳定性.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com